Background
The group's work on triggering in thermoacoustics showed that there is little point considering the non-normal behaviour of a thermoacoustic system until one has mapped out its nonlinear behaviour. At the time, we were expecting this nonlinear behaviour to be periodic. A visiting student, Giovanni Campa, showed that these periodic solutions could be found with a thermoacoustic network model:
Obtaining bifurcation diagrams with a thermoacoustic network model
G. Campa and M. P. Juniper
ASME Turbo Expo, Copenhagen, Denmark, 11-15 June 2012, GT2012-68241, (2012)
pdf
Linear techniques can predict whether the non-oscillating (steady) state of a thermoacoustic system is stable or unstable. With a sufficiently large impulse, however, a thermoacoustic system can reach a stable oscillating state even when the steady state is also stable. A nonlinear analysis is required to predict the existence of this oscillating state. Continuation methods are often used for this but they are computationally expensive.
In this paper, an acoustic network code called LOTAN is used to obtain the steady and the oscillating solutions for a horizontal Rijke tube. The heat release is modelled as a nonlinear function of the mass flow rate. Several test cases from the literature are analysed in order to investigate the effect of various nonlinear terms in the flame model. The results agree well with the literature, showing that LOTAN can be used to map the steady and oscillating solutions as a function of the control parameters. Furthermore, the nature of the bifurcation between steady and oscillating states can be predicted directly from the nonlinear terms inside the flame model.
Dynamical Systems approach to thermoacoustics
This technique, however, can only use a simple nonlinear saturation model for the flame. In most thermoacoustic systems, the most influential nonlinearity is due to the flame -- i.e. not due to the gas dynamics or the damping. We therefore wanted to include more complex flame behaviour than a simple saturation model. We did this by creating a nonlinear dynamical system consisting of a flame simulation bolted to a state-space acoustic model:
Finding thermoacoustic limit cycles for a ducted Burke-Schumann flame
S. Illingworth, I. Waugh, M. Juniper
Proceedings of the Combustion Institute 34 911--920 (2012) doi:10.1016/j.proci.2012.06.017
pdf
doi: https://doi.org/10.1016/j.proci.2012.06.017
This paper examines nonlinear thermoacoustic oscillations of a ducted Burke?Schumann diffusion flame. The nonlinear dynamics of the thermoacoustic system are studied using two distinct approaches. In the first approach, a continuation analysis is performed to find limit cycle amplitudes over a range of operating conditions. The strength of this approach is that one can characterize the coupled system?s nonlinear behaviour over a large parameter space with relative ease. It is not able to give physical insight into that behaviour, however. The second approach uses a Flame Describing Function (FDF) to characterize the flame?s response to harmonic velocity fluctuations over a range of forcing frequencies and forcing amplitudes, from which limit cycle amplitudes can be found. A strength of the FDF approach is that it reveals the physical mechanisms responsible for the behaviour observed. However, the calculation of the FDF is time consuming, and it must be recalculated if the flame?s operating conditions change. With the strengths and shortcomings of the two approaches in mind, this paper advocates combining the two to provide the dynamics over a large parameter space and, furthermore, physical insight into that behaviour at judiciously-chosen points in the parameter space. Further physical insight concerning the flame?s near-linear response at all forcing amplitudes is given by studying the forced flame in the time domain. It is shown that, for this flame model, the limit cycles arise because of the flame?s nonlinear behaviour when it is close to the inlet.
Acoustic state-space models using a wave-based approach
S. Illingworth, M. P. Juniper
21st International Congress on Sound and Vibration, Beijing, China, 13-17 July 2014, (2014)
pdf
A wave-based analysis is a convenient method for generating acoustic models, both for simple and for more complex geometries. However, there is no straightforward method to describe the resulting system in state-space form. This prevents powerful, well-established methods from dynamics and control being applied to a wave-based acoustic model because these methods require a state-space description of the system to which they are applied. This paper presents a simple method for generating a state-space description of an acoustic model when that model has been derived using a wave-based approach. The utility of the method is demonstrated by applying it to a simple open-ended duct with a temperature jump across the flame, and the resulting state-space model is validated in both the time domain and the frequency domain. The method is sufficiently general that it can also be applied to more complex geometries.
We then used continuation methods to find limit cycles of these nonlinear dynamical systems, starting with a diffusion flame:
Limit cycle of a Burke-Schumann flame in a tube
This video shows a thermoacoustic limit cycle of a Burke-Schumann (diffusion) flame in a tube found using matrix-free continuation methods. The top two frames show the acoustic pressure and velocity fields in the tube. The tube has open ends so there is a pressure node and a velocity antinode at each end. The Burke-Schumann flame sits in the black box at x = 1. This field is expanded in the bottom frame. The bottom frame shows the perturbation mixture fraction field (colours) and the flame position (black line).
Credit: Iain Waugh and Simon Illingworth
Jump to publication (will be at top of next screen)
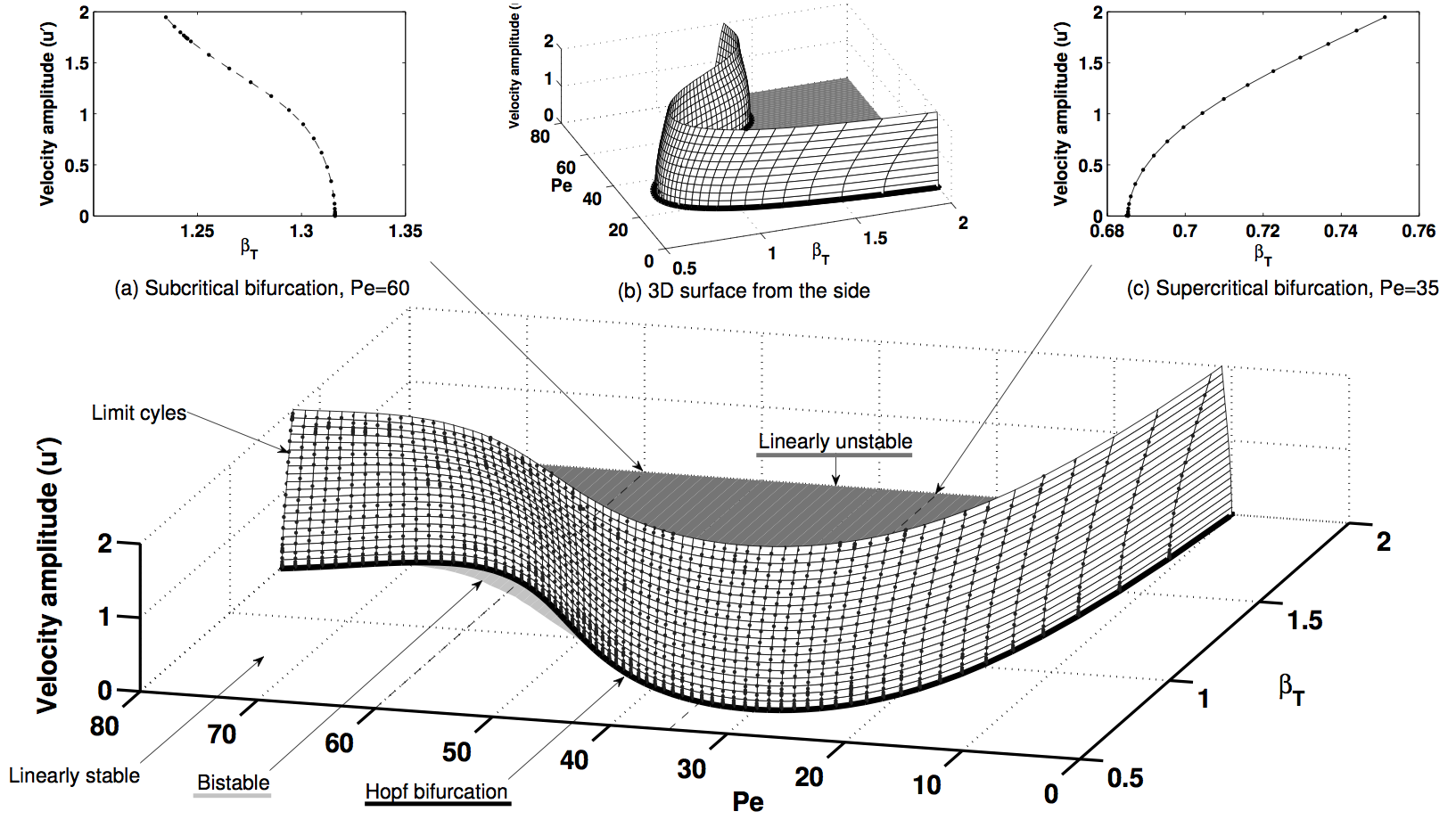
Bifurcation diagram of a Burke-Schumann flame in a tube
The bottom diagram shows the maximum velocity amplitude for limit cycles of a Burke-Schumann flame in a tube, as a function of Peclet number (Pe) and heat release parameter (beta). These are calculated with matrix-free continuation methods. The top-left frame shows a cut at Pe=60, revealing a subcritical bifurcation. The top=right frame shows a cut through Pe=30, revealing a supercritical bifurcation.
Credit: Iain Waugh and Simon Illingworth
Jump to publication (will be at top of next screen)
Matrix-free continuation for bifurcation analysis of large thermoacoustic systems
I. C. Waugh, S. Illingworth, M. Juniper
Journal of Computational Physics 240 183--202 (2013) doi:10.1016/j.jcp.2012.12.034
pdf
doi: https://doi.org/10.1016/j.jcp.2012.12.034
In order to define the nonlinear behaviour of a thermoacoustic system, it is important to find the regions of parameter space where limit cycles exist. Continuation methods find limit cycles numerically in the time domain, with no additional assumptions other than those used to form the governing equations. Once the limit cycles are found, these continuation methods track them as the operating condition of the system changes.
Most continuation methods are impractical for finding limit cycles in large thermoacoustic systems because the methods require too much computational time and memory. In the literature, there are therefore only a few applications of continuation methods to thermoacoustics, all with low-order models.
Matrix-free shooting methods efficiently calculate the limit cycles of dissipative systems and have been demonstrated recently in fluid dynamics, but are as yet unused in thermoacoustics. These matrix-free methods are shown to converge quickly to limit cycles by implicitly using a ?reduced order model? property. This is because the methods preferentially use the influential bulk motions of the system, whilst ignoring the features that are quickly dissipated in time.
The matrix-free methods are demonstrated on a model of a ducted 2D diffusion flame, and the stability limits are calculated as a function of the Peclet number and the heat release parameter. Both subcritical and supercritical Hopf bifurcations are found. Physical information about the flame-acoustic interaction is found from the limit cycles and Floquet modes. Invariant subspace preconditioning, higher order prediction techniques, and multiple shooting techniques are all shown to reduce the time required to generate bifurcation surfaces. Two types of shooting are compared, and two types of matrix-free evaluation are compared.
The diffusion flame was a poor choice, however, because its behaviour is almost completely linear. The only source of nonlinear saturation is due to the flame being unable to pass back through the injection plane. We therefore turned to a model of a ducted premixed flame already being developed by Karthik Kashinath. We used a G-equation approach (using LSGEN, from Santosh Hemchandra), which was capable of simulating flame wrinkling and pinch-off:
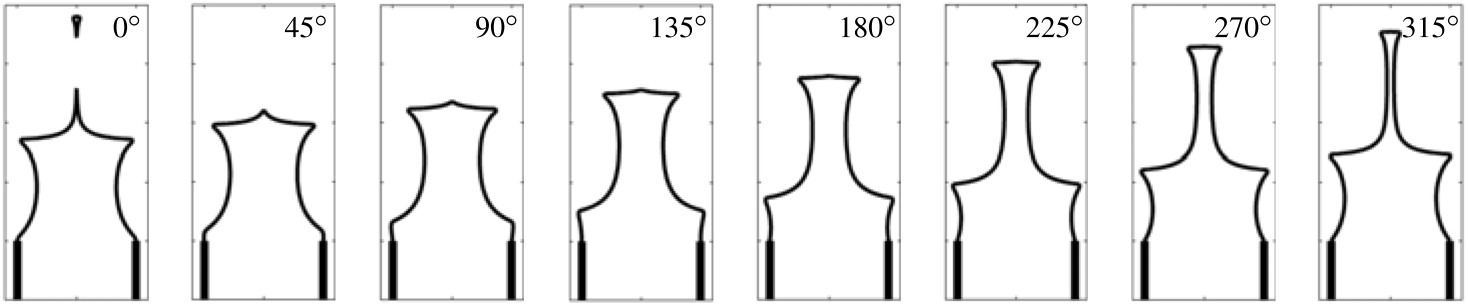
Snapshots of a harmonically-forced G-equation flame
These are snapshots of a G-equation (pre-mixed) flame when the velocity field is forced harmonically. The G-equation formulation permits the flame to wrinkle, form cusps, and pinch off.
Credit: Karthik Kashinath
This permitted much more elaborate nonlinear behaviour and we successfully found a wide variety of periodic solutions:
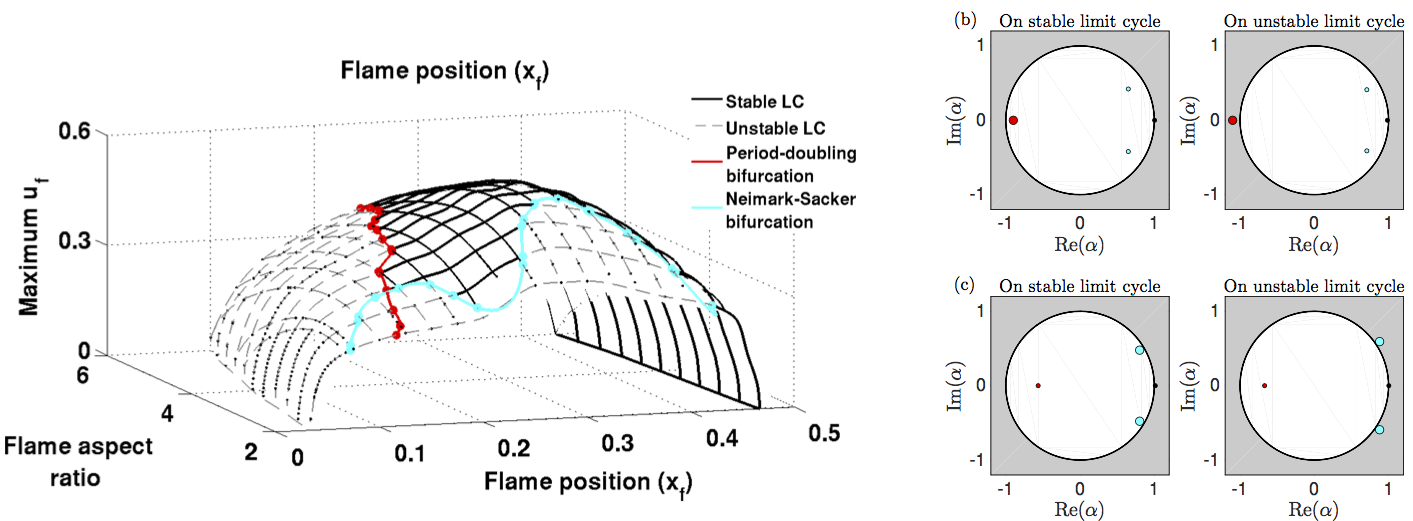
Bifurcation diagram and Floquet multipliers of a G-equation flame in a tube
The left diagram shows the bifurcation diagram for periodic thermoacoustic oscillations of a conical G-equation (premixed) bunsen flame in a tube. These oscillations are found with a continuation methods as a function of the flame aspect ratio and the flame position in the duct. The stability of these oscillations is determined by examining the Floquet multipliers, alpha. For a period-doubling bifurcation (top right), a Floquet multiplier (red dot) crosses the unit circle at alpha = -1. For a Neimark-Sacker bifurcation to quasiperiodic behaviour, a pair or Floquet multipliers (cyan dots) cross the unit circle at Im(alpha) not equal to zero. The analysis reveals that periodic solutions are often unstable.
Credit: Iain Waugh
Jump to publication (will be at top of next screen)
Matrix-free continuation of limit cycles and their bifurcations for a ducted premixed flame
I. C. Waugh, K. Kashinath and M. P. Juniper
Journal of Fluid Mechanics 759 1--27 (2014) doi:10.1017/jfm.2014.549
pdf
Open Access
doi: https://doi.org/10.1017/jfm.2014.549
Many experimental studies have demonstrated that ducted premixed flames exhibit stable limit cycles in some regions of parameter space. Recent experiments have also shown that these (period-1) limit cycles subsequently bifurcate to period-2n, quasiperiodic, multiperiodic or chaotic behaviour. These secondary bifurcations cannot be found computationally using most existing frequency domain methods, because these methods assume that the velocity and pressure signals are harmonic. In an earlier study we have shown that matrix-free continuation methods can efficiently calculate the limit cycles of large thermoacoustic systems. This paper demonstrates that these continuation methods can also efficiently calculate the bifurcations from the limit cycles. Furthermore, once these bifurcations are found, it is then possible to isolate the coupled flame?acoustic motion that causes the qualitative change in behaviour. This information is vital for techniques that use selective damping to move bifurcations to more favourable locations in the parameter space. The matrix-free methods are demonstrated on a model of a ducted axisymmetric premixed flame, using a kinematic G-equation solver. The methods find limit cycles and period-2 limit cycles, and fold, period-doubling and Neimark?Sacker bifurcations as a function of the location of the flame in the duct, and the aspect ratio of the steady flame.
Continuation methods have the advantage that one can easily perform a stability analysis (specifically a Floquet analysis) around the periodic solutions that have been found. All types of bifurcation can be identified: period-1 (which is the only type that can be identified with a Flame Describing Function approach), period-2 (which give rise to a period doubling bifurcation), and Neimark-Sacker (which give rise to quasiperiodicity). We therefore found continuation methods to be very attractive from a scientific point of view. They are also relatively cheap if one wishes to examine a single flame-network combination. However, if one wishes to examine the behaviour of a given flame inside many different acoustic networks, then a Flame Describing Function method is cheaper. It is important to consider, however, whether the FDF method will give reliable results:
When will a flame describing function approach to thermoacoustics work well?
S. Illingworth and M. P. Juniper
Int. Conf. on Sound and Vibration, Vilnius, Lithuania, 08-12 July 2012, (2012)
pdf
In any thermoacoustic analysis, it is important not only to predict linear frequencies and growth rates, but also the amplitude and frequencies of any limit cycles. The Flame Describing Function (FDF) approach is a quasi-linear analysis which allows the prediction of both the linear and nonlinear behaviour of a thermoacoustic system. This means that one can predict linear growth rates and frequencies, and also the amplitudes and frequencies of any limit cycles. The FDF achieves this by assuming that the acoustics are linear and that the flame, which is the only nonlinear element in the thermoacoustic system, can be adequately described by considering only its response at the frequency at which it is forced. Therefore any harmonics generated by the flame's nonlinear response are not considered. This implies that these nonlinear harmonics are small or that they are sufficiently filtered out by the linear dynamics of the system (the low-pass filter assumption). In this paper, a flame model with a simple saturation nonlinearity is coupled to simple duct acoustics, and the success of the FDF in predicting limit cycles is studied over a range of flame positions and acoustic damping parameters. Although these two parameters affect only the linear acoustics and not the nonlinear flame dynamics, they determine the validity of the low-pass filter assumption made in applying the flame describing function approach. Their importance is highlighted by studying the level of success of an FDF-based analysis as they are varied. This is achieved by comparing the FDF?s prediction of limit-cycle amplitudes to the amplitudes seen in time domain simulations.
Identifying elaborate nonlinear behaviour
If periodic solutions are unstable, continuation methods can calculate the type of instability growing around the periodic solution. However, they cannot calculate the fully nonlinear behaviour. Brute force nonlinear simulations are required for this. Karthik Kashinath performed a large number of such simulations for a ducted premixed flame and found many examples of elaborate nonlinear behaviour:
Nonlinear self-excited thermoacoustic oscillations of a ducted premixed flame: bifurcations and routes to chaos
K. Kashinath, I. C. Waugh, M. P. Juniper
Journal of Fluid Mechanics 761 399--430 (2014) doi:10.1017/jfm.2014.601
pdf
Open Access
doi: https://doi.org/10.1017/jfm.2014.601
Thermoacoustic systems can oscillate self-excitedly, and often non-periodically, owing to coupling between unsteady heat release and acoustic waves. We study a slot-stabilized two-dimensional premixed flame in a duct via numerical simulations of a G-equation flame coupled with duct acoustics. We examine the bifurcations and routes to chaos for three control parameters: (i) the flame position in the duct, (ii) the length of the duct and (iii) the mean flow velocity. We observe period-1, period-2, quasi-periodic and chaotic oscillations. For certain parameter ranges, more than one stable state exists, so mode switching is possible. At intermediate times, the system is attracted to and repelled from unstable states, which are also identified. Two routes to chaos are established for this system: the period-doubling route and the Ruelle?Takens?Newhouse route. These are corroborated by analyses of the power spectra of the acoustic velocity. Instantaneous flame images reveal that the wrinkles on the flame surface and pinch-off of flame pockets are regular for periodic oscillations, while they are irregular and have multiple time and length scales for quasi-periodic and aperiodic oscillations. This study complements recent experiments by providing a reduced-order model of a system with approximately 5000 degrees of freedom that captures much of the elaborate nonlinear behaviour of ducted premixed flames observed in the laboratory.
The tools used to analyse the time series data are in the supplementary materials of the ARFM paper below, co-authored with R. I. Sujith.
Figure 10 of the above paper shows phase portraits and Poincare sections for period-1, period-2, quasiperiodic, period-5, and chaotic oscillations. Figures 12 and 13 show that the route taken by the dynamical system passes close to several unstable attractors before it reaches a stable attractor:
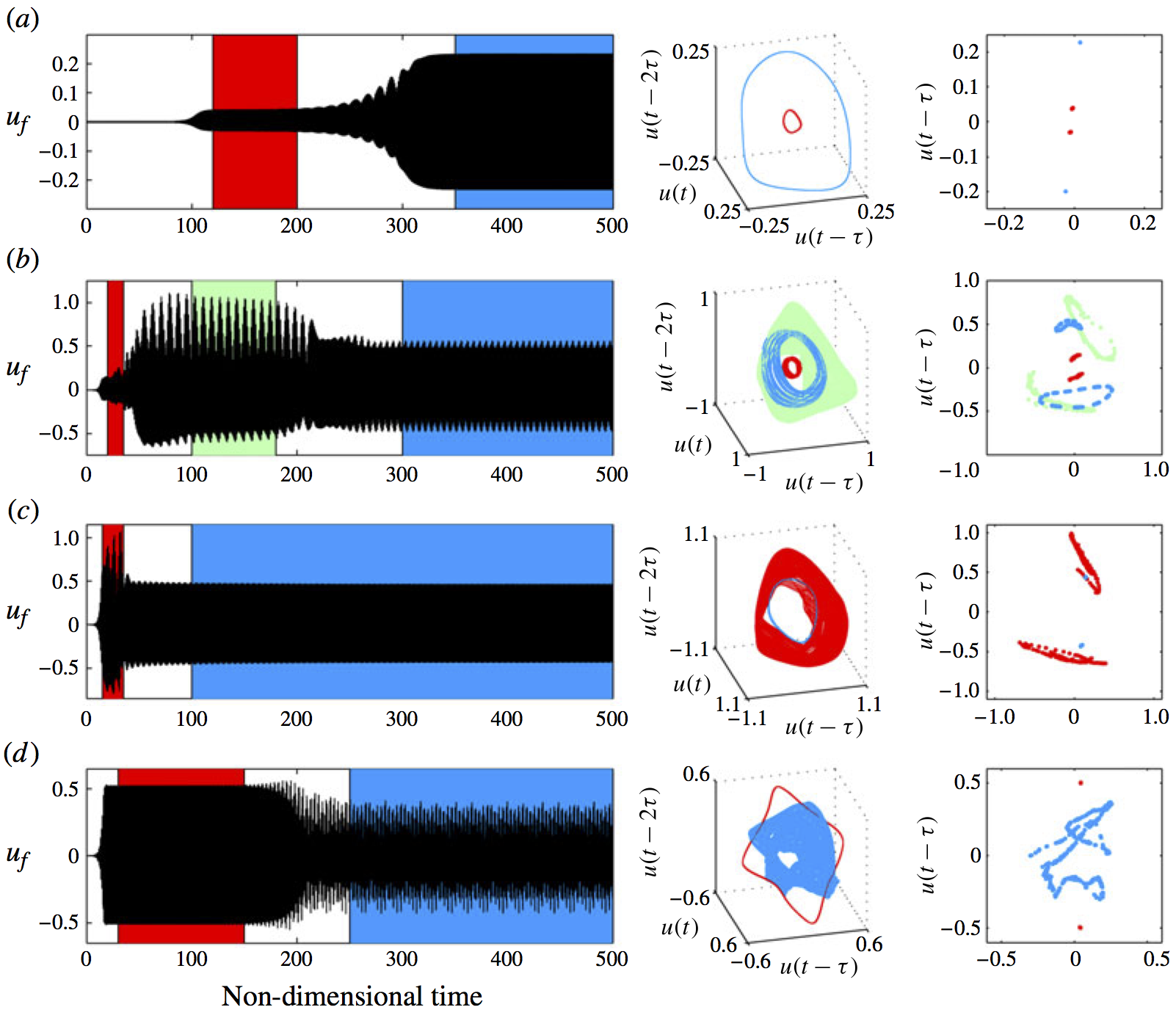
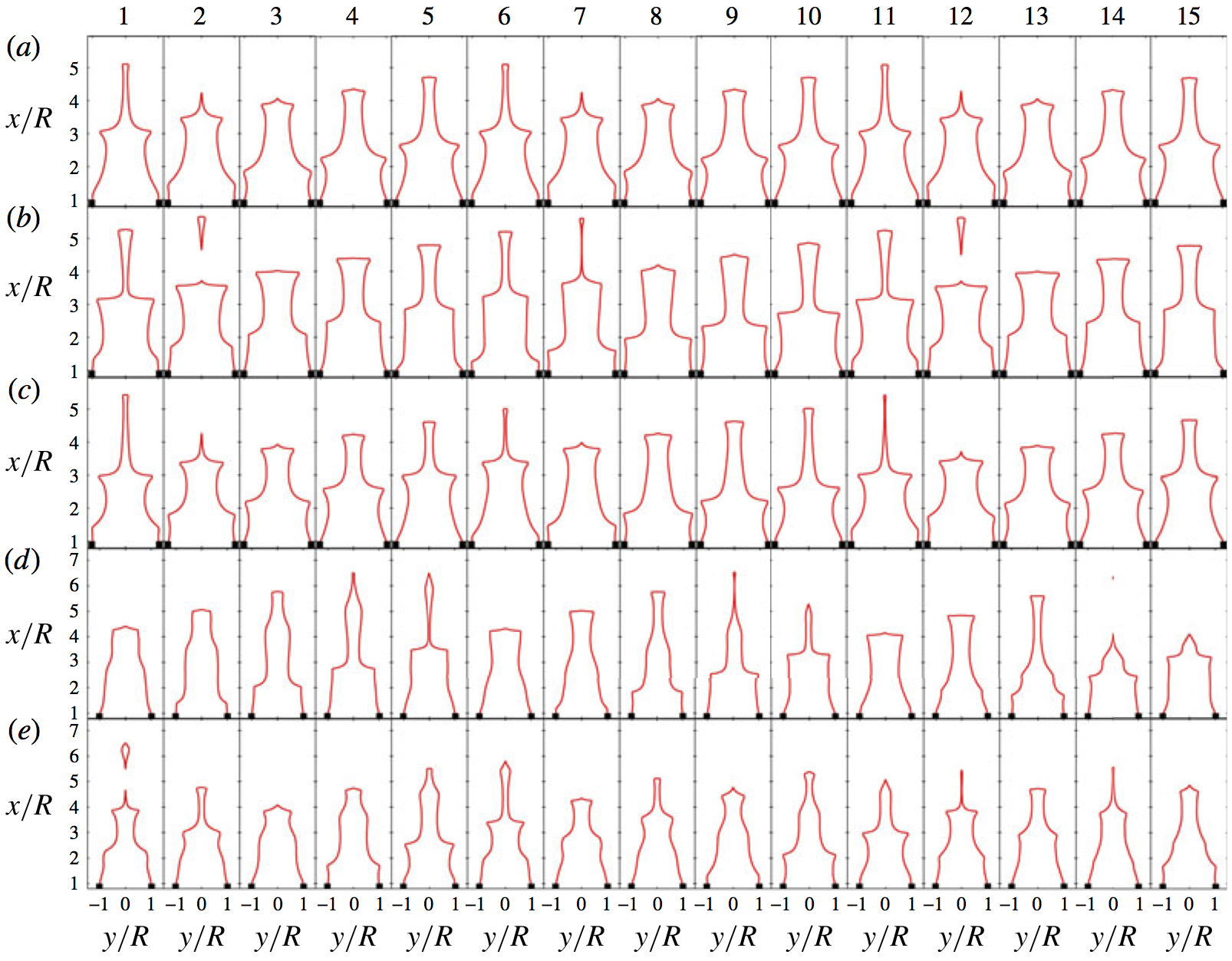
Trajectories of linearly unstable thermoacoustic systems containing G-equation flames (Fig 12)
Time series (left), phase portraits (middle), and Poincare maps (right) of the velocity signal for thermoacoustic oscillations of a G-equation flame in a tube. These show: (a) transition to a stable periodic solution (blue) via an unstable periodic solution (red), which is unstable to a quasiperiodic motion; (b) transition to a stable quasiperiodic solution (blue) via two unstable quasiperiodic solutions (blue and green); (c) transition to a stable periodic solution (blue) via an unstable quasiperiodic solution (red); (d) transition to a stable quasiperiodic solution (blue) via an unstable periodic solution (red).
Credit: Karthik Kashinath
Jump to publication (will be at top of next screen)
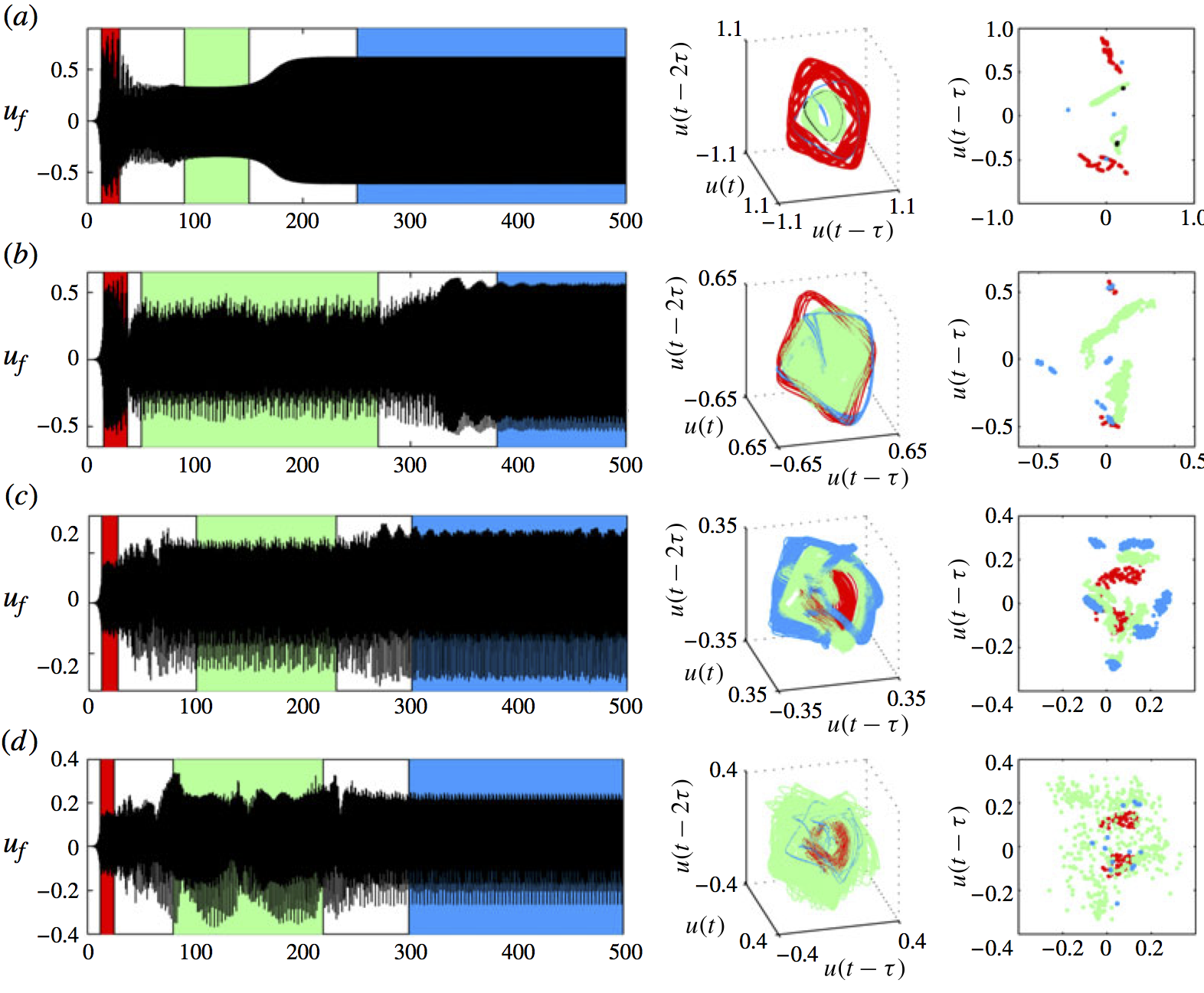
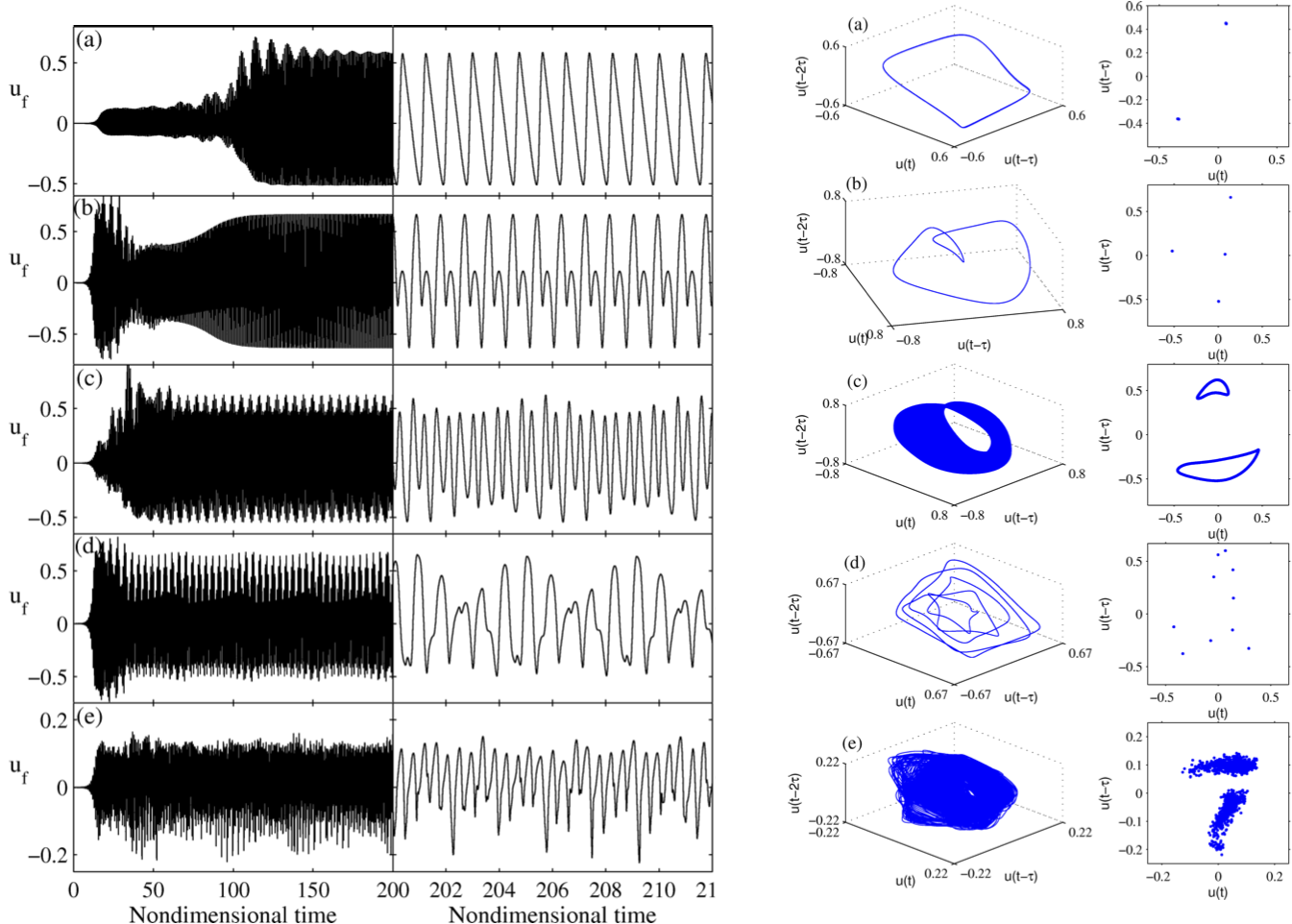
Trajectories of linearly unstable thermoacoustic systems containing G-equation flames (Fig 13)
Time series (left), phase portraits (middle), and Poincare maps (right) of the velocity signal for thermoacoustic oscillations of a G-equation flame in a tube. These show: (a) transition to a stable period 2 solution via two unstable quasiperiodic solutions (red and green); (b) transition to a stable period 2 solution via an unstable quasiperiodic solution (red) and an unstable chaotic solution (green); (c) transition to a stable chaotic solution (blue) via two unstable chaotic solutions (red and green); (d) transition to a stable period-k solution via two unstable chaotic solutions (red and green).
Credit: Karthik Kashinath
Jump to publication (will be at top of next screen)
This is directly analogous to bypass transition to turbulence in hydrodynamics. Figure 3 shows that, for given parameters, there can be more than one stable attractor. Finally, figure 14 shows a period-doubling route to chaos and figure 15 shows a Ruelle-Takens-Newhouse route to chaos:
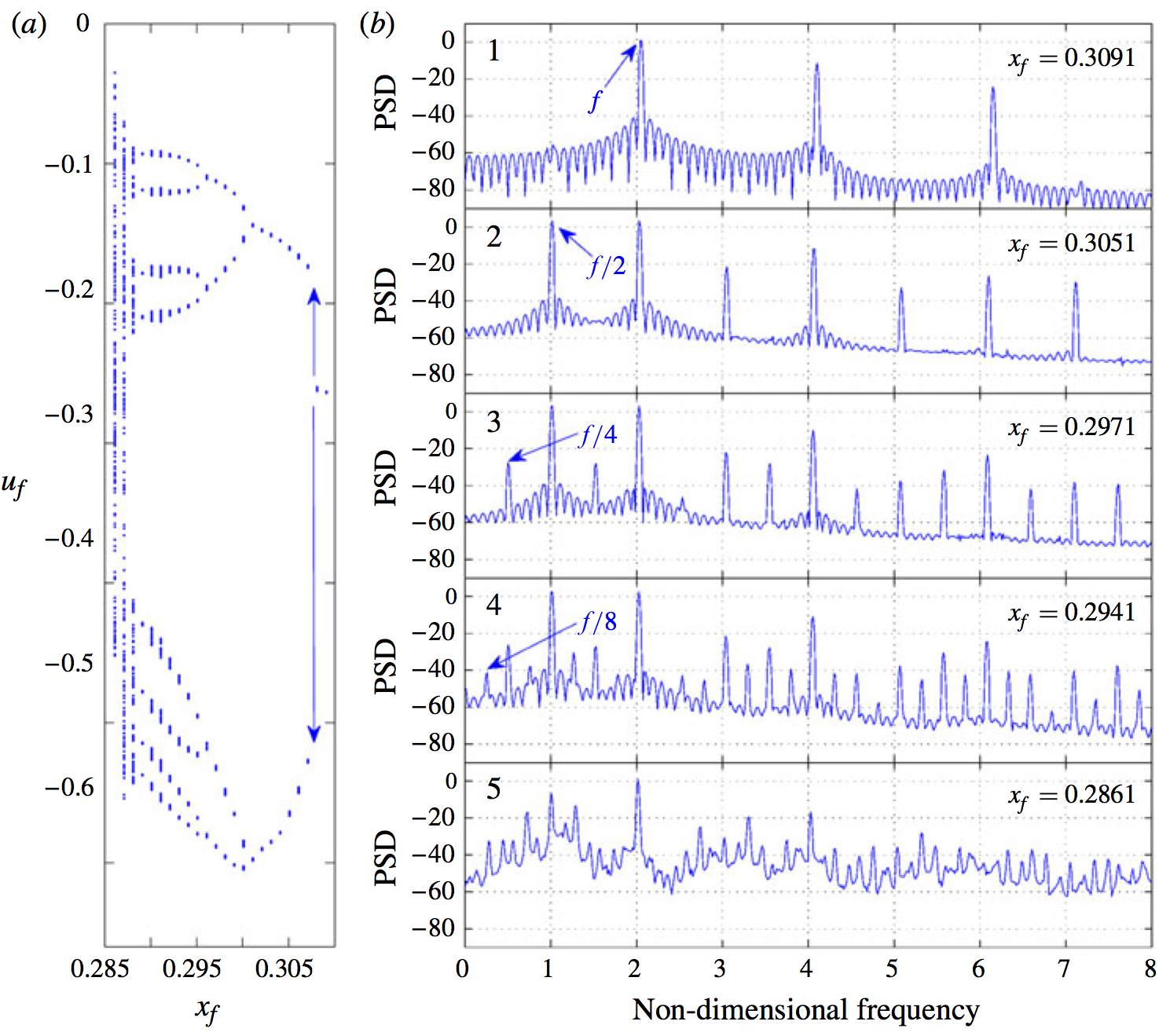
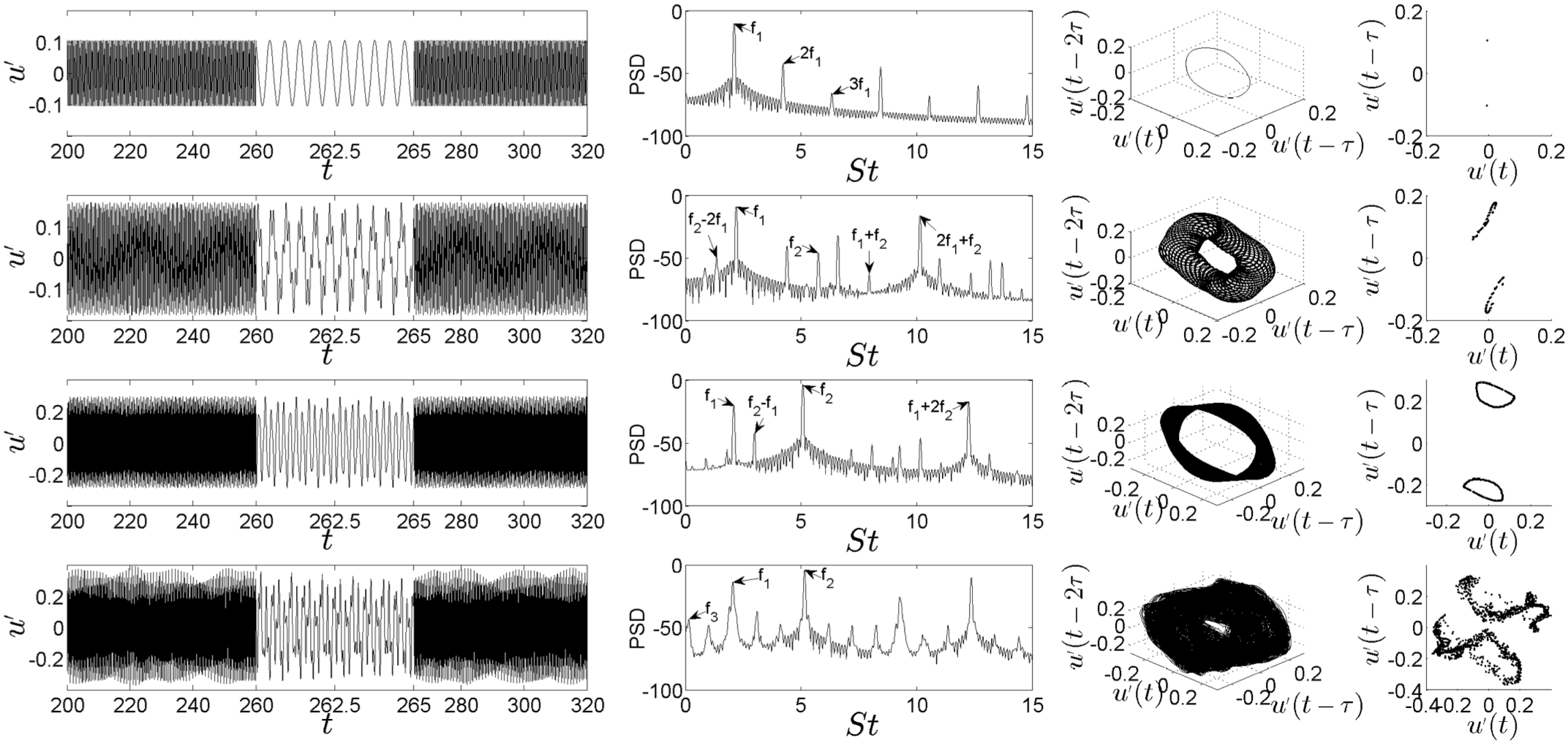
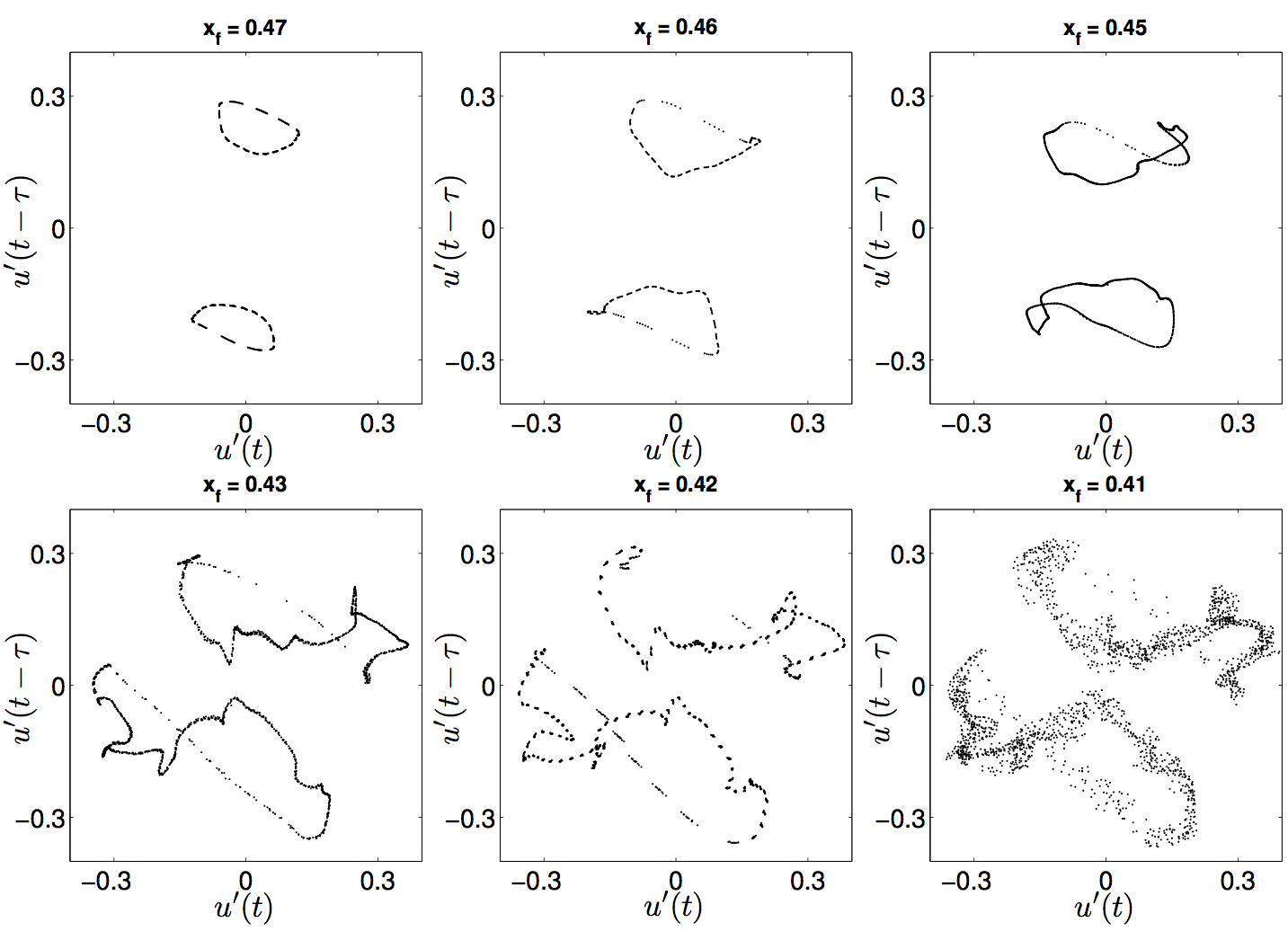
Period-doubling route to chaos observed in a thermoacoustic system containing a G-equation flame (Fig 14)
The bifurcation diagram on the left shows the negative peaks of the acoustic velocity as the location of a G-equation flame is varied within a tube. At x_f = 0.3091, these peaks pass through the same point at u_f = -0.27, showing that the solution is periodic. This can be seen clearly in the top-right figure, which shows the power spectral density (PSD) as a function of frequency. As x_f reduces, the system passes through a period-doubling bifurcation, shown by the appearance of two peaks in the bifurcation diagram and a frequency at f/2 in the PDS. A cascade of period-doubling bifurcations ensues, ending up with a chaotic oscillation.
Credit: Karthik Kashinath
Jump to publication (will be at top of next screen)
The complete bifurcation diagram is:
This is described in more detail in this conference presentation:
All this elaborate nonlinear behaviour arises from a simple premixed bunsen-like flame in a duct. The results compare well with the experimental results of Kabiraj and Sujith (e.g. J. Engineering for Gas Turbines and Power 134, 031502)
The above behaviour was for a flame in a simple duct. Our next activity was to incoporate an acoustic network model so that complex acoustic geometries could be considered:
Frequency domain and time domain analysis of thermoacoustic oscillations with wave-based acoustics
A. Orchini, S. Illingworth, M. P. Juniper
Journal of Fluid Mechanics 775 387--414 (2015) doi:10.1017/jfm.2015.139
pdf
Open Access
doi: https://doi.org/10.1017/jfm.2015.139
Many thermoacoustic systems exhibit rich nonlinear behaviour. Recent studies show that this nonlinear dynamics can be well captured by low-order time domain models that couple a level set kinematic model for a laminar flame, the G-equation, with a state-space realization of the linearized acoustic equations. However, so far the G-equation has been coupled only with straight ducts with uniform mean acoustic properties, which is a simplistic configuration. In this study, we incorporate a wave-based model of the acoustic network, containing area and temperature variations and frequency-dependent boundary conditions. We cast the linear acoustics into state-space form using a different approach from that in the existing literature. We then use this state-space form to investigate the stability of the thermoacoustic system, both in the frequency and time domains, using the flame position as a control parameter. We observe frequency-locked, quasiperiodic, and chaotic oscillations. We identify the location of Neimark?Sacker bifurcations with Floquet theory. We also find the Ruelle?Takens?Newhouse route to chaos with nonlinear time series analysis techniques. We highlight important differences between the nonlinear response predicted by the frequency domain and the time domain methods. This reveals deficiencies with the frequency domain technique, which is commonly used in academic and industrial studies of thermoacoustic systems. We then demonstrate a more accurate approach based on continuation analysis applied to time domain techniques.
We then went on to show that the open-loop application of harmonic acoustic forcing can be an effective strategy for controlling periodic or aperiodic thermoacoustic oscillations. In some cases, we find that such forcing can reduce the response amplitude by up to 90%, making it a viable way to weaken thermoacoustic oscillations
Forced synchronization of periodic and aperiodic thermoacoustic oscillations: lock-in, bifurcations, and open-loop control
K. Kashinath, L. K. B. Li, M. P. Juniper
Journal of Fluid Mechanics 838 690--714 (2018) doi:10.1017/jfm.2017.879
pdf
Open Access
doi: https://doi.org/10.1017/jfm.2017.879
Synchronization is a universal concept in nonlinear science but has received little attention in thermoacoustics. In this numerical study, we take a dynamical systems approach to investigating the influence of harmonic acoustic forcing on three different types of self-excited thermoacoustic oscillations: periodic, quasiperiodic and chaotic.
When the periodic system is forced, we find that (i) at low forcing amplitudes, it responds at both the forcing frequency and the natural (self-excited) frequency, as well as at their linear combinations, indicating quasiperiodicity; (ii) above a critical forcing amplitude, the system locks into the forcing; (iii) the bifurcations leading up to lock-in and the critical forcing amplitude required for lock-in depend on the proximity of the forcing frequency to the natural frequency; (iv) the response amplitude at lock-in may be larger or smaller than that of the unforced system and the system can exhibit hysteresis and the jump phenomenon owing to a cusp catastrophe; and (v) at forcing amplitudes above lock-in, the oscillations can become unstable and transition to chaos, or switch between different stable attractors depending on the forcing amplitude.
When the quasiperiodic system is forced at a frequency equal to one of the two characteristic frequencies of the torus attractor, we find that lock-in occurs via a saddle node bifurcation with frequency pulling. When the chaotic system is forced at a frequency close to the dominant frequency of its strange attractor, we find that it is possible to destroy chaos and establish stable periodic oscillations.
These results show that the open-loop application of harmonic acoustic forcing can be an effective strategy for controlling periodic or aperiodic thermoacoustic oscillations. In some cases, we find that such forcing can reduce the response amplitude by up to 90%, making it a viable way to weaken thermoacoustic oscillations.
The Flame Double Input Describing Function
We also compared frequency-domain techniques (i.e. the Flame Describing Function, FDF) with time-domain techniques (i.e. continuation methods and time-marching). Where the nonlinear behaviour was quasiperiodic or chaotic, the single input FDF techniques did not predict the range of amplitudes well. We then performed a very large number of simulations and generated a double input FDF, which is the response of the flame to forcing at two different frequencies, each over a range of forcing amplitudes. This could predict the locations of Neimark-Sacker bifurcations to quasiperiodicity:

Bifurcation diagram calculated with a Flame Double Input Describing Function
The Flame Describing Function encapsulates a flame's response to harmonic forcing at a given frequency and amplitude. It can be used to estimate the amplitude of thermoacoustic periodic solutions but cannot predict quasiperiodic oscillations. We implemented the
double input describing function, which encapsulates the flame's response to two independent harmonic forcing signals at different amplitudes and frequencies. This is considerably more expensive to obtain but can predict the onset and amplitude of quasiperiodic oscillaitons:
Credit: Alessandro Orchini
Jump to publication (will be at top of next screen)
Flame double input describing function analysis
A. Orchini, M. P. Juniper
Combustion and Flame 171 87--102 (2016) doi:10.1016/j.combustflame.2016.06.014
pdf
Open Access
doi: https://doi.org/10.1016/j.combustflame.2016.06.014
The Flame Describing Function (FDF) is a useful and relatively cheap approximation of a flame's nonlinearity with respect to harmonic velocity fluctuations. When embedded into a linear acoustic network, it is able to predict the amplitude and stability of harmonic thermoacoustic oscillations through the harmonic balance procedure. However, situations exist in which these oscillations are not periodic, but their spectrum contains peaks at several incommensurate frequencies. If one assumes that two frequencies dominate the spectrum, these oscillations are quasiperiodic, and the FDF concept can be extended by forcing the flame with two amplitudes and two frequencies. The nonlinearity is then approximated by a Flame Double Input Describing Function (FDIDF), which is a more expensive object to calculate than the FDF, but contains more information about the nonlinear response.
In this study, we present the calculation of a non-static flame's FDIDF. We use a G-equation-based laminar conical flame. We embed the FDIDF into a thermoacoustic network and we predict the nature and amplitude of thermoacoustic oscillations through the harmonic balance method. A criterion for the stability of these oscillations is outlined. We compare our results with a classical FDF analysis and self-excited time domain simulations of the same system. We show how the FDIDF improves the stability prediction provided by the FDF. At a numerical cost roughly equivalent to that of two FDFs, the FDIDF is capable to predict the onset of Neimark-Sacker bifurcations and to identify the frequency of oscillations around unstable limit cycles. At a higher cost, it can also saturate in amplitude these oscillations and predict the amplitude and stability of quasiperiodic oscillations.
Weakly nonlinear analysis and Annular Combustors
The group's work on triggering showed that it is very important to discover whether a Hopf bifurcation (which is from linearly stable to oscillating behaviour) is supercritical or subcritical. For supercritical Hopf bifurcations, the oscillation amplitude grows smoothly from zero. For subcritical Hopf bifurcations, the oscillation amplitude grows abruptly, which can be dangerous:
Triggering in thermoacoustics
M. P. Juniper
International Journal of Spray and Combustion Dynamics 4 (3) 217--238 (2012)
pdf
Under certain conditions, the flow in a combustion chamber can sustain large amplitude oscillations even when its steady state is linearly stable. Experimental studies show that these large oscillations can sometimes be triggered by very low levels of background noise. This theoretical paper sets out the conditions that are necessary for triggering to occur. It uses a weakly nonlinear analysis to show when these conditions will be satisfied for cases where the heat release rate is a function of the acoustic velocity. The role played by non-normality is investigated. It is shown that, when a state triggers to sustained oscillations from the lowest possible energy, it exploits transient energy growth around an unstable limit cycle. The positions of these limit cycles in state space is determined by nonlinearity, but the tangled-ness of trajectories in state space is determined by non-normality. When viewed in this dynamical systems framework, triggering in thermoacoustics is seen to be directly analogous to bypass transition to turbulence in pipe flow.
The above paper contains a rudimentary weakly nonlinear analysis around the Hopf bifurcation. Alessandro Orchini and George Rigas performed a more complete weakly nonlinear analysis of a thermoacoustic system, with wave acoustics and a heat release model for a hot wire:
Weakly nonlinear analysis of thermoacoustic bifurcations in the Rijke tube
A. Orchini, G. Rigas, M. P. Juniper
Journal of Fluid Mechanics 805 523--550 (2016) doi:10.1017/jfm.2016.585
pdf
Open Access
doi: https://doi.org/10.1017/jfm.2016.585
In this study we present a theoretical weakly nonlinear framework for the prediction of thermoacoustic oscillations close to Hopf bifurcations. We demonstrate the method for a thermoacoustic network that describes the dynamics of an electrically heated Rijke tube. We solve the weakly nonlinear equations order by order, discuss their contribution on the overall dynamics, and show how solvability conditions at odd orders give rise to Stuart?-Landau equations. These equations, combined together, describe the nonlinear dynamical evolution of the oscillations amplitude and their frequency. Because we retain the contribution of several acoustic modes in the thermoacoustic system, the use of adjoint methods is required to derive the Landau-coefficients. The analysis is performed up to fifth order and compared with time domain simulations, showing good agreement. The theoretical framework presented here can be used to reduce the cost of investigating oscillations and subcritical phenomena close to Hopf bifurcations in numerical simulations and experiments, and can be readily extended to consider, e.g., the weakly nonlinear interaction of two unstable thermoacoustic modes.
Weakly nonlinear analysis can also be applied to annular combustors. In these combustors, waves can travel in both directions around the annulus, meaning that eigenvalues are degenerate (for the case with zero mean flow) or nearly degenerate (when there is mean flow). An important practical question is whether the stable state of the system exhibits standing waves or spinning waves. The analysis in the following paper is somewhat different from that in the preceding papers. It calculates the conditions under which fully-developed spinning and/or standing thermoacoustic oscillations will be stable, given the configuration of the flames and their Describing Functions:
Weakly nonlinear analysis of thermoacoustic instabilities in annular combustors
G. Ghirardo, M. P. Juniper, J. Moeck
Journal of Fluid Mechanics 805 52--87 (2016) doi:10.1017/jfm.2016.494
pdf
Open Access
doi: https://doi.org/10.1017/jfm.2016.494
Rotationally symmetric annular combustors are of practical importance because they generically resemble combustion chambers in gas turbines, in which thermoacoustically driven oscillations are a major concern. We focus on azimuthal thermoacoustic oscillations and model the fluctuating heat release rate as being dependent only on the local pressure in the combustion chamber. We study the dynamics of the annular combustor with a finite number of compact flames equispaced around the annulus, and characterize the flames? response with a describing function. We discuss the existence, amplitude and the stability of standing and spinning waves, as a function of: 1) the number of the burners; 2) the acoustic damping in the chamber; 3) the flame response. We present the implications for industrial applications and the future direction of investigations. We then present as an example the first theoretical study of thermoacoustic triggering in annular combustors, which shows that rotationally symmetric annular chambers that are thermoacoustically unstable do not experience only stable spinning solutions, but can also experience stable standing solutions. We finally test the theory on one experiment with good agreement.
An earlier study showed that standing modes tend to be favoured if the Flame Describing Function's amplitude reduces in response to transverse forcing.
Azimuthal instabilities in annular combustors: standing and spinning modes
G. Ghirardo, M. P. Juniper
Proceedings of the Royal Society A. 469 20130232 (2013) doi:10.1098/rspa.2013.0232
pdf
doi: https://doi.org/10.1098/rspa.2013.0232
This theoretical study investigates spinning and standing modes in azimuthally symmetric annular combustion chambers. Both modes are observed in experiments and simulations, and an existing model predicts that spinning modes are the only stable state of the system. We extend this model to take into account the effect that the acoustic azimuthal velocity, u, has on the flames, and propose a phenomenological model based on experiments performed on transversely forced flames. This model contains a parameter, delta, that quantifies the influence that the transversal excitation has on the fluctuating heat release. For small values of delta, spinning modes are the only stable state of the system. In an intermediate range of delta, both spinning and standing modes are stable states. For large values of delta, standing modes are the only stable state. This study shows that a flame?s response to azimuthal velocity fluctuations plays an important role in determining the type of thermoacoustic oscillations found in annular combustors.
A further study used the G-equation method to develop Flame Describing Functions for an M-shaped flame. These are particularly easy to interpret when the FDF is expressed as a sum of time delays - the flame behaviour can be explained with just two time delays.
G-equation modelling of thermo-acoustic oscillations of partially-premixed flames
B. Semlitsch, A. Orchini, A. P. Dowling, M. P. Juniper
International Journal of Spray and Combustion Dynamics 9 (4) 260--276 (2017) doi:10.1177/1756827717711405
pdf
Open Access
doi: https://doi.org/10.1177/1756827717711405
Numerical simulations aid combustor design to avoid and reduce thermo-acoustic oscillations. Nonlinear heat release rate estimation and its modelling are essential for the prediction of saturation amplitudes of limit cycles. The heat release dynamics of flames can be approximated by a Flame Describing Function (FDF). To calculate an FDF, a wide range of forcing amplitudes and frequencies needs to be considered. For this reason, we present a computationally inexpensive level-set approach, which accounts for equivalence ratio perturbations on flames with arbitrarily-complex shapes. The influence of flame parameters and modelling approaches on flame describing functions and time delay coefficient distributions are discussed in detail. The numerically-obtained flame describing functions are compared with experimental data and used in an acoustic network model for limit cycle prediction. A reasonable agreement of the heat release gain and limit cycle frequency is achieved even with a simplistic, analytical velocity fluctuation model. However, the phase decay is over-predicted. For sophisticated flame shapes, only the realistic modelling of large-scale flow structures allows the correct phase decay predictions of the heat release rate response.