
Some flows contain large regions of absolute instability, which makes them globally unstable. They oscillate at well-defined frequencies. Two well-known examples are a helium jet discharging into air and the flow around a bluff body, such as a cylinder:
There is a common misconception that globally unstable flows are insensitive to forcing. Although this is true for a linear analysis, for which the long time behaviour is dominated by the intrinsic frequency (the saddle point), it is not true in a nonlinear analysis or in nature. In a series of careful experiments, Larry Li and I forced a naturally-oscillating helium jet at various frequencies and amplitudes and compared the resultant motion with that of a forced van der Pol oscillator.
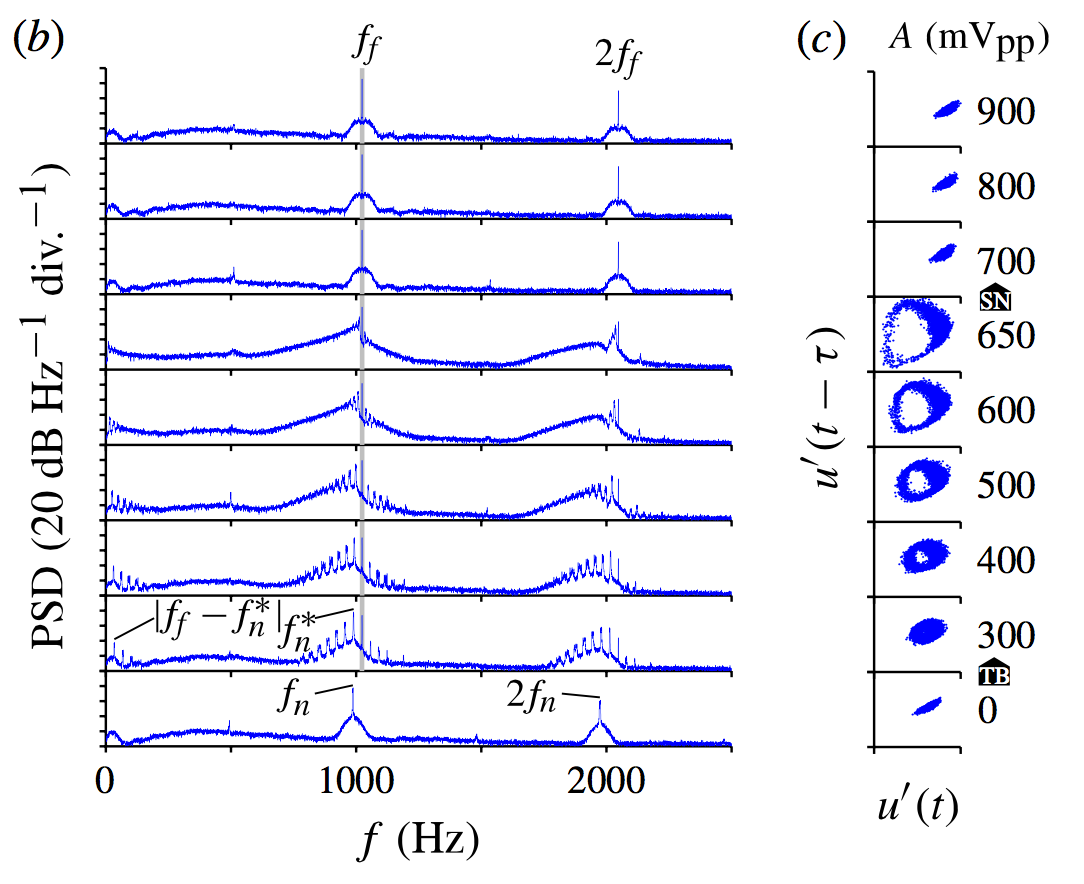
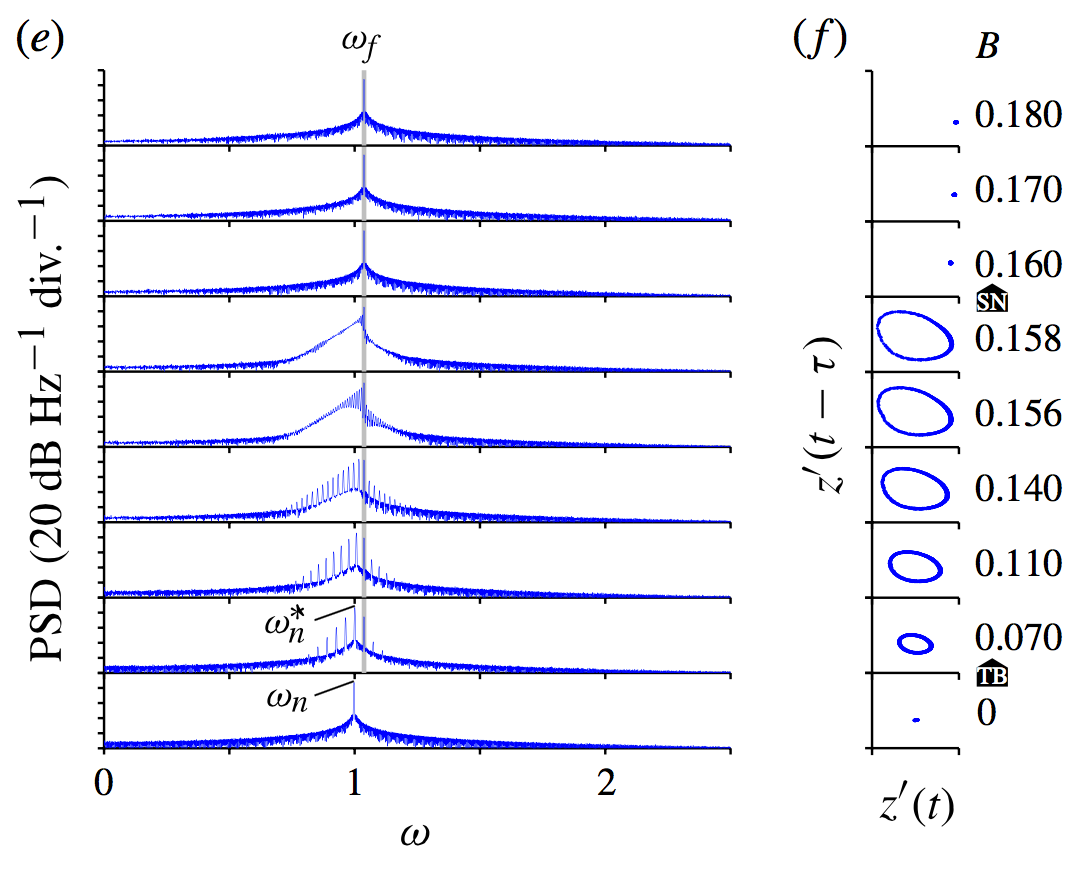
The behaviour around the fundamental frequency (1000 Hz) is qualitatively identical (note that the van der Pol oscillator has only odd-numbered overtones). Full details are in this paper:
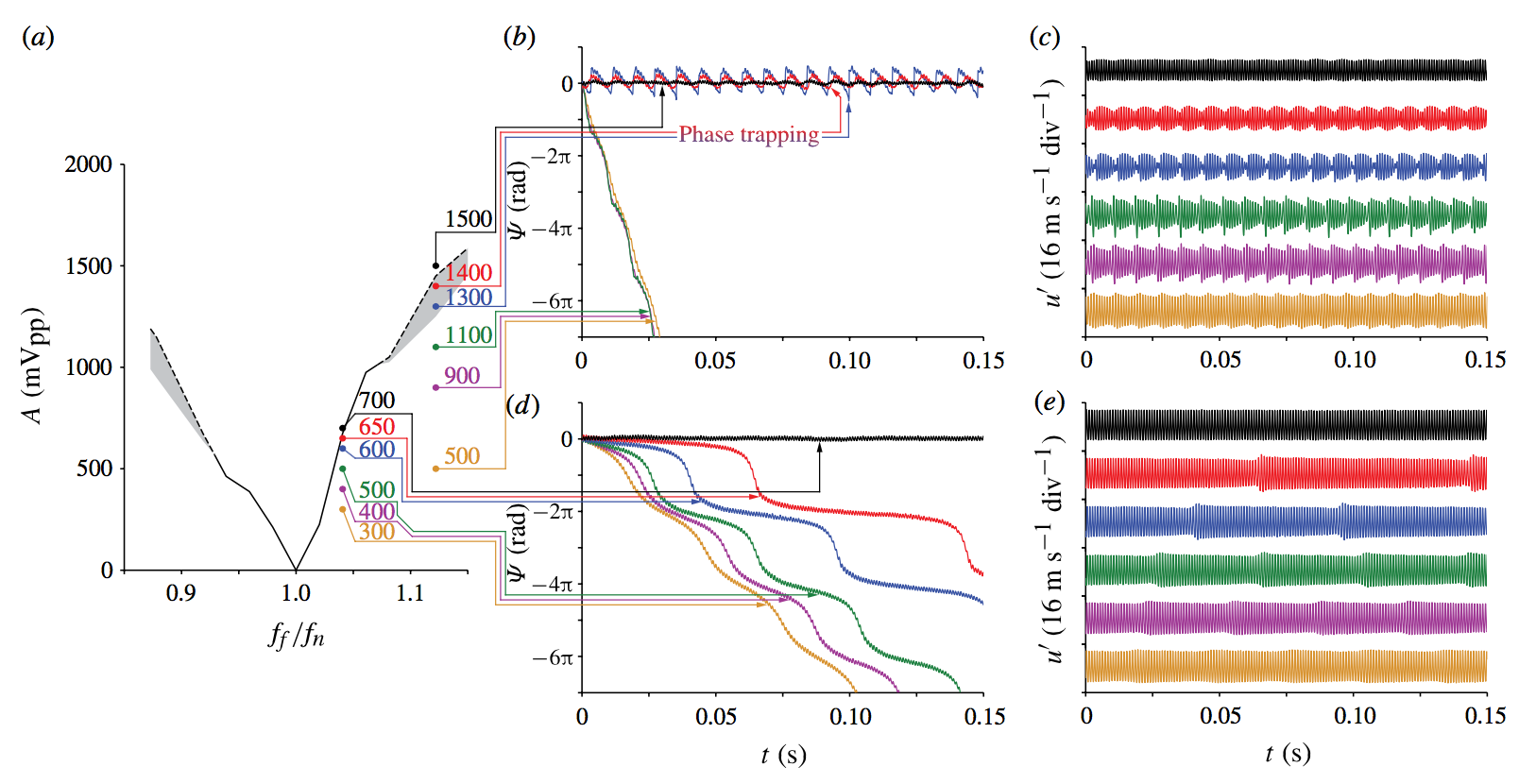
Figures 6, 7, 10, and 11 of the above paper show the behaviour most clearly. When the jet is forced at low amplitudes, its response is quasiperiodic (in inexact terms, this corresponds to a response at both the forcing and the natural frequencies). When the jet is forced at high amplitudes, its response locks into the forcing frequency. The exact sequence of bifurcations follows that which is observed for the forced van der Pol oscillator, which can be identified with hand calculations (see Blanov et al. Synchronization; from Simple to Complex, Springer). We also observed phase trapping and slipping in our experimental measurements. These had been observed experimentally in lasers, but not before in hydrodynamics:
The above experiments were performed on helium jets, which have a strong but short region of absolute instability at their base. In an earlier study, we had examined jet diffusion flames, which have a strong and long region of absolute instability in their outer plume.

In that study, we found that the natural mode could dominate in the downstream region, even if the upstream region was oscillating at the forcing frequency. This is an interesting result because it shows that strong absolute instability could weaken the feedback loop that causes thermoacoustic oscillations.
In this experimental and numerical study, two types of round jet are examined under acoustic forcing. The first is a non-reacting low density jet (density ratio 0.14). The second is a buoyant jet diffusion flame at a Reynolds number of 1100 (density ratio of unburnt fluids 0.5). Both jets have regions of strong absolute instability at their base and this causes them to exhibit strong self-excited bulging oscillations at well-defined natural frequencies. This study particularly focuses on the heat release of the jet diffusion flame, which oscillates at the same natural frequency as the bulging mode, due to the absolutely unstable shear layer just outside the flame.
The jets are forced at several amplitudes around their natural frequencies. In the non-reacting jet, the frequency of the bulging oscillation locks into the forcing frequency relatively easily. In the jet diffusion flame, however, very large forcing amplitudes are required to make the heat release lock into the forcing frequency. Even at these high forcing amplitudes, the natural mode takes over again from the forced mode in the downstream region of the flow, where the perturbation is beginning to saturate non-linearly and where the heat release is high. This raises the possibility that, in a flame with large regions of absolute instability, the strong natural mode could saturate before the forced mode, weakening the coupling between heat release and incident pressure perturbations, hence weakening the feedback loop that causes combustion instability.
These experiments inspired us to examine the nonlinear behaviour of thermoacoustic systems. This data was also used in one of the first papers on the Dynamic Mode Decomposition