High performance rocket engines, such as those in the Space Shuttle and Ariane V, burn liquid oxygen (LOx) and gaseous hydrogen (GH2). The injectors sit in the top of the combustion chamber and, for maximum combustion efficiency, the fuels must burn before they reach the throat of the nozzle.
The LOx tube sits within the GH2 tube and experiments have shown that combustion efficiency is improved if the LOx tube is recessed inside the GH2 tube (see above image). In 1978, Gill had proposed a mechanism for this (G. Gill, 1978 A qualitative technique for concentric tube element optimization, utlilizing the factor dynamic head ratio-1, AIAA Paper 78–76). We started this project with the thought that combustion within the recessed region would increase the dynamic head ratio and therefore the atomization efficiency and combustion efficiency.
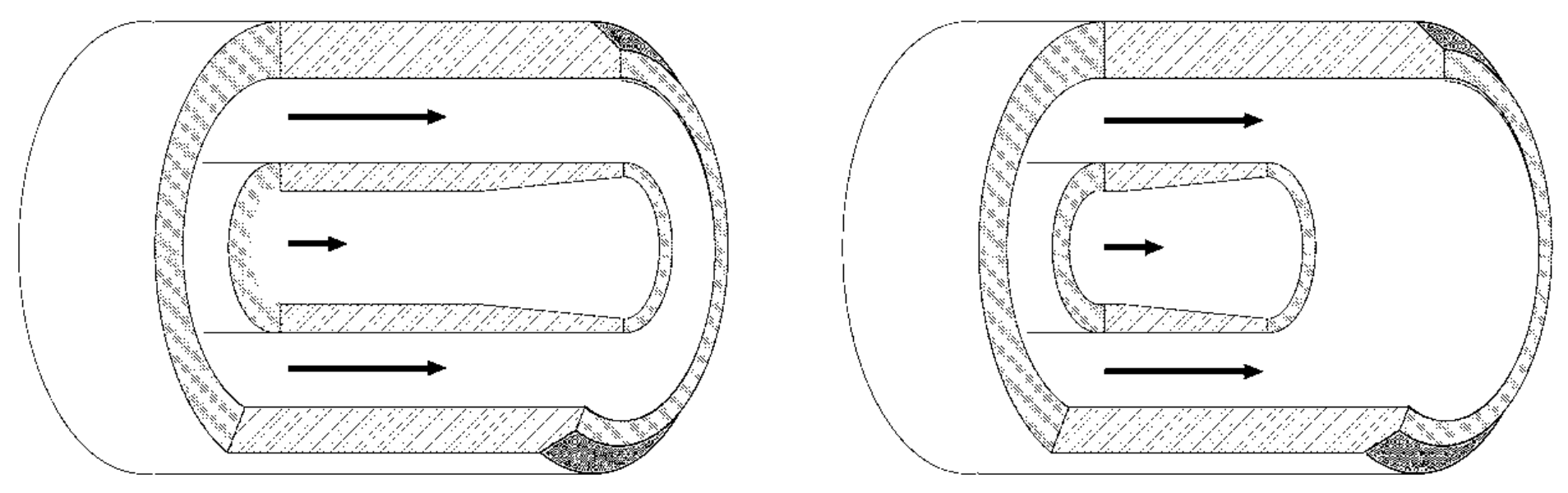
Recessed coaxial injector
Rocket engines often use coaxial fuel injectors, in which liquid Oxygen is injected through the central tube while gaseous hydrogen is injected through the outer annulus. Experiments show that the combustion efficiency improves if the central tube is recessed within the outer tube.
Credit: Matthew Juniper
Jump to publication (will be at top of next screen)
This, however, turned out to make little difference, as shown in section 3.6 of my thesis:
Structure and Stabilization of Cryogenic Spray Flames
M. P. Juniper
Ecole Centrale de Paris, (2001), examined by S. Candel, N. Darabiha, E. Hopfinger, G. Searby, J-L Thomas, P. Vuillermoz, V. Yang, S. Zaleski
pdf
Open Access
The success of a satellite launcher depends to a great extent on its efficiency and reliability. Engines using cryogenic fuels, such as liquid oxygen and hydrogen, are used for most missions since they combine high performance with a relatively light structure. The design of such motors has, until recently, been based on empirical results from systematic tests. Future design will rely on numerical simulations and will envisage alternative reactant combinations, such as methane and oxygen. The definition of entry conditions to these numerical simulations requires a knowledge of the flame structure, particularly of the region near the fuel injectors. These practical considerations motivate this investigation.
As well as discussion on the overall flame shape under subcritical and supercritical conditions, two aspects are given special attention: (1) the injector geometry, (2) stabilization of the flame. The latter question is critical for the system's reliability and is particularly important when considering fuels which are less reactive than hydrogen and oxygen.
Systematic experiments are performed at up to 70 bar pressure on a coaxial fuel injector similar to those used in current mototrs. Optical diagnostics combined with image processing yield the flame structure. Models are then developed regarding the effect of injector geometry and tested against experimental results from this and other coaxial injectors. In this manner the physical mechanisms controlling flame shape are deduced. A result of scientific interest is that a wake flow, consisting of a slow stream within a faster stream, is more unstable when enclosed within a duct. This provides one possible mechanism for the effect of recess on the cryogenic flame.
The question of stabilization is approached in carefully-defined stages so that model problems from the field of combustion science can be applied. First the base of the flame is divided into two parts and one is treated as a counterflow diffusion flame above a condensed surface. Numerical simulations performed here add new results to the study of this configuration. The second part of the base is treated initially as a corner flame, a model problem which has been investigated only recently. Two parameters controlling the shape of the flame are defined and the relationship between them is deduced from nuerical simulations. This approach permits a simple progression to more complex geometries. The flames above a porous plate with fuel injection and then above a vaporizing reactant are considered. Finally, the situation of a flame behind a step over a vaporizing reactant is analysed. This is a realistic model of the base of a cyrogenic spray flame. Through this progression the non-dimensional parameters governing behaviour are introduced successively and the most influential parameters are identified. The final result will aid design both of the engine and the control sequences of ignition, leading to enhanced reliability.
Instead, we discovered that the confining walls could be creating a local region of absolute instability in the recessed portion, triggering a flapping wake mode, causing the LOx jet to break up in a shorter distance:
The Stability of Ducted Compound Flows and Consequences for the Geometry of Coaxial Injectors
M. P. Juniper, S. M. Candel
Journal of Fluid Mechanics 482 257--269 (2003) doi:10.1017/S0022112003004075
pdf
doi: https://doi.org/10.1017/S0022112003004075
A two-dimensional wake-like compound flow, formed by a low-speed stream embedded within a high-speed flow, is examined in this article. It is shown that the range of absolutely unstable flow in parameter space greatly increases when such a flow is confined within a duct. Parameters studied here are: the density ratio, which is from 0.1 to 1000; the velocity ratio, which varies from co-flow to counter-flow; and the ratio of the duct width to the width of the central jet. Absolutely unstable flows permit perturbations to propagate upstream, and can lead to self-sustained global oscillations similar to the vortex shedding process which takes place in the wake of a bluff body. This theoretical situation models the wake-like behaviour of a two-fluid coaxial injector with a recessed central tube. The aerodynamic destabilizing mechanism is of primary importance whereas the stabilizing mechanisms, which are not considered here, are of secondary importance. The conclusions from this analysis of a ducted compound flow can explain why one observes self-sustained oscillations in recessed coaxial injectors. The presence of a recirculation bubble in the central flow, which is the basis of other proposed explanations, is not required.
Although the above paper correctly identified the mechanism, the analysis was rudimentary. I later performed a more careful analysis on general 2D planar jets and wakes and showed that the strong instability was caused by resonance between the inner and outer flows:
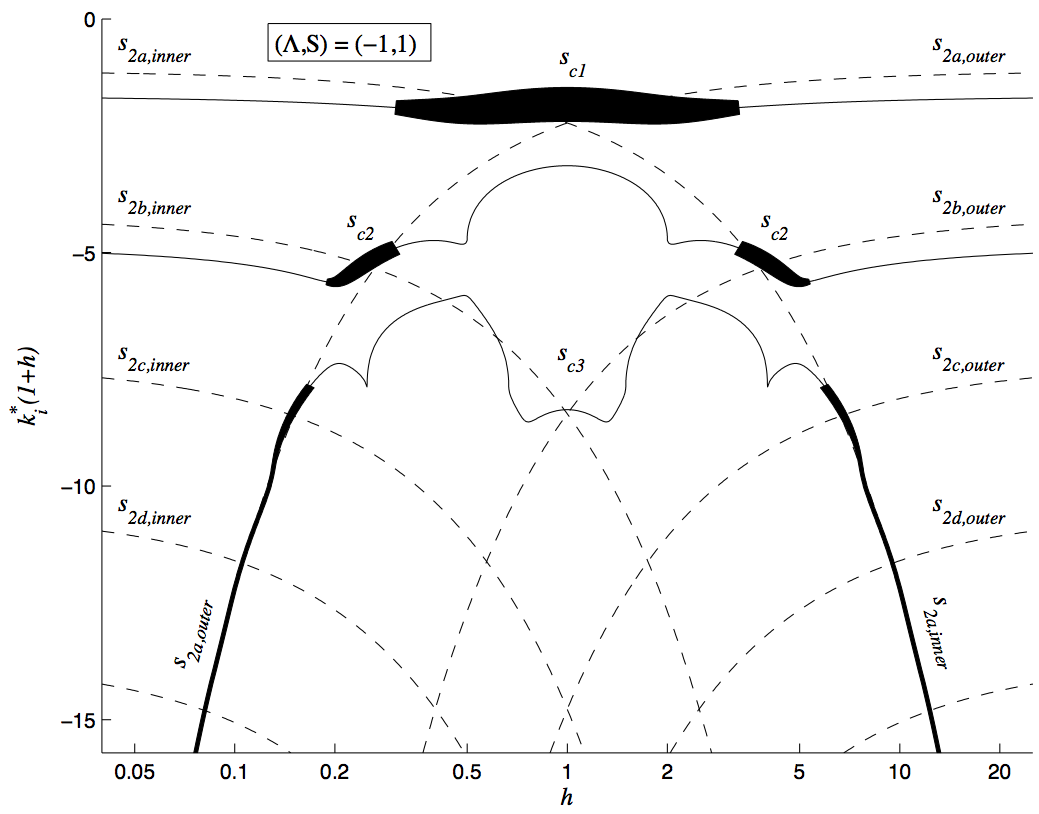
Sinuous instability of confined flows
Cross-stream wavenumber (k_i) of the most unstable wave with zero group velocity as a function of confinement ratio, h, for sinuous motion of a confined wake flow. The thickness of the line is proportional to the growth rate. The dashed lines show the value of k_i for modes in the inner flow and outer flow if the other flow were not present. This shows that the confined flow is most unstable at values of h at which the modes in the inner flow and outer flow have the same cross-stream wavenumber, which is at h=1 for sinuous wake flows.
Credit: Matthew Juniper
Jump to publication (will be at top of next screen)
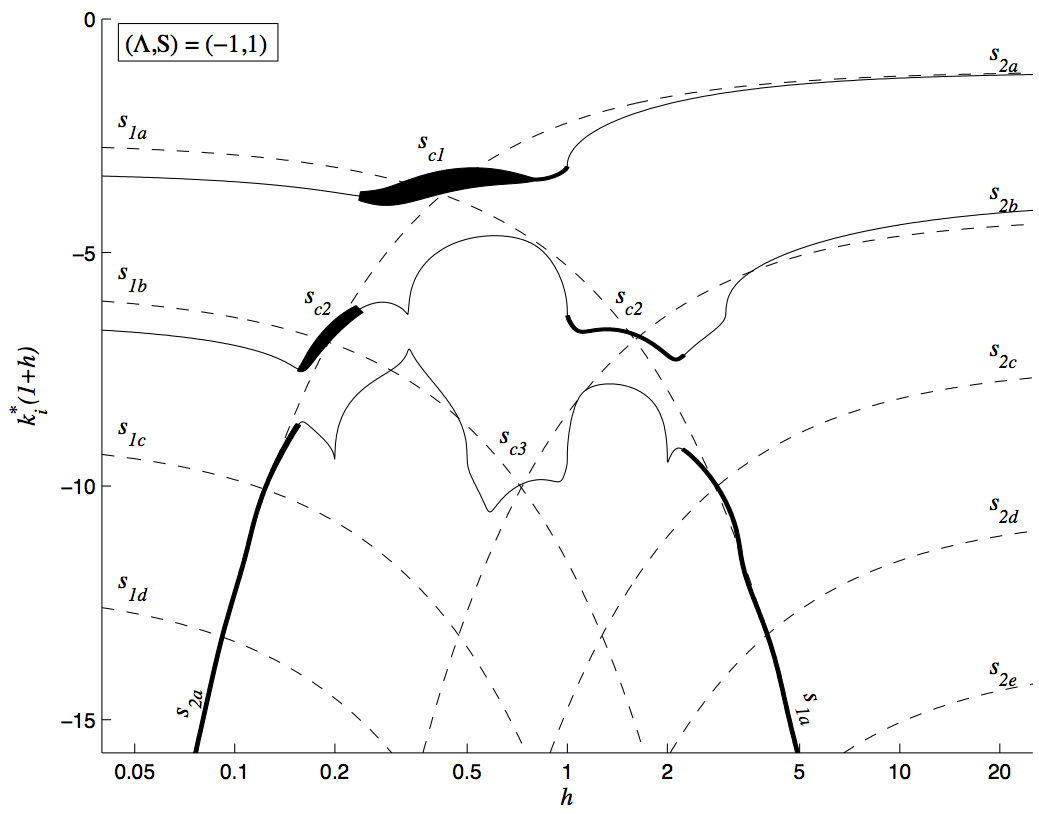
Varicose instability of confined flows
Cross-stream wavenumber (k_i) of the most unstable wave with zero group velocity as a function of confinement ratio, h, for varicose motion of a confined wake flow. The thickness of the line is proportional to the growth rate. The dashed lines show the value of k_i for modes in the inner flow and outer flow if the other flow were not present. This shows that the confined flow is most unstable at values of h at which the modes in the inner flow and outer flow have the same cross-stream wavenumber.
Credit: Matthew Juniper
Jump to publication (will be at top of next screen)
This is described in:
The Effect of Confinement on the Stability of Two-dimensional Shear flows
M. Juniper
Journal of Fluid Mechanics 565 171--195 (2006) doi:10.1017/S0022112006001558
pdf
doi: https://doi.org/10.1017/S0022112006001558
It has been shown recently that the instability of a two-dimensional wake increases when it is confined in the transverse direction by two flat plates. Confinement causes the transition from convective to absolute instability to occur at lower values of shear. This paper examines this effect comprehensively and concludes that it is due to the constructive interaction of modes with zero group velocity in the wake (or jet) and in the surrounding flow. Maximum instability occurs when the wavenumber of the fundamental mode in the wake (or jet) matches that of the funda- mental mode in the surrounding flow. Other regions of high instability occur when the harmonics of one mode interact with the fundamental of the other. This effect is examined at density ratios from 0.001 to 1000. At each density ratio, the confinement which causes maximum absolute instability can be predicted. This study also shows that it is vital to examine the wavenumber of absolutely unstable modes in order to avoid over-predicting the absolute instability. In some situations this wavenumber is vanishingly small and the mode must be discounted on physical grounds.
When performing this analysis, I found that, for unconfined flows, the most unstable saddle point would sometimes cross into the half-plane where k_r is less than 0. At the time, I presumed that this made it an invalid k+/k- pinch point and discounted it. Simultaneously, however, Jonathan Healey had found similar behaviour in the rotating disk boundary layer (Healey, J. J., 2006, J. Fluid Mech. 560, 279--310). He had correctly interpreted it as a physically consistent mode with growth away from the plate and had also correctly shown that this explained why confinement causes a flow to become more absolutely unstable (Healey, J. J., 2007, J. Fluid Mech. 579, 29-61). Consequently, I revised this aspect of the analysis carefully:
The full impulse response of two-dimensional shear flows and implications for confinement
M. Juniper
Journal of Fluid Mechanics 590 163--185 (2007) doi:10.1017/S0022112007007975
pdf
doi: https://doi.org/10.1017/S0022112007007975
In this theoretical study, a linear spatio-temporal analysis is performed on unconfined and confined inviscid jet/wake flows in order to determine whether they are absolutely or convectively unstable. The impulse response is evaluated in the entire outer fluid, rather than just at the point of impulse, over a wide range of density ratios. This confirms that the dominant saddle point can validly migrate into the plane of diverging eigenfunctions. This reveals that, at certain density ratios and shear numbers, the response can grow upstream in some directions with a cross-stream component, even though it decays directly upstream of, and at, the point of impulse. This type of flow is convectively unstable when unconfined, but becomes absolutely unstable when confined. Other effects of confinement are described in a previous paper. Together, these articles have important implications for the design of fuel injectors, which often employ confined shear flows at high Reynolds number and large density ratios to generate strong mixing in combustion chambers.
The next steps were to repeat this analysis for 2D axisymmetric (i.e. round) flows:
The effect of confinement on the stability of non-swirling round jet/wake flows
M. Juniper
Journal of Fluid Mechanics 605 227--252 (2008) doi:10.1017/S0022112008001547
pdf
doi: https://doi.org/10.1017/S0022112008001547
It has recently been shown that the instability characteristics of planar jets and wakes change when the flows are confined between two flat plates. This is due to constructive interaction between modes with zero group velocity in the inner and outer flows. In this theoretical study, a linear spatio-temporal analysis is performed on unconfined and confined round jets and wakes in order to discover whether the same effect is observed. There are several similarities between the planar case and the round case as well as some significant differences. Nevertheless, the effect of confinement on round flows is found to be very similar to that on planar flows and to act via the same physical mechanism. This paper examines density ratios from 0.001 to 1000 and has important implications for the design of fuel injectors, which often employ confined shear flows at high Reynolds numbers and large density ratios to generate strong mixing in combustion chambers.
and then with surface tension and viscosity:
The effect of surface tension on the stability of unconfined and confined planar jets and wakes
S. J. Rees, M. P. Juniper
Journal of Fluid Mechanics 633 71--97 (2009) doi:10.1017/S0022112009007186
pdf
doi: https://doi.org/10.1017/S0022112009007186
In this theoretical study, a linear spatio-temporal analysis is performed on unconfined and confined inviscid jet/wake flows with surface tension in order to determine convective/absolute instability criteria. There is a single mode that is due to surface tension and many modes that are due to the jet/wake column. In the unconfined case, the full impulse response is considered in the entire outer flow. On the one hand, the surface tension mode propagates slowly in the cross-stream direction but dominates at the front and back of the wavepacket. On the other hand, the jet/wake column modes propagate more quickly in the cross-stream direction and therefore define the boundaries of the central region of the wavepacket. The flow is particularly unstable when these modes interact. For unconfined flows, it is found that at low and intermediate surface tensions the flow can be more absolutely unstable than that without surface tension but at high surface tensions the flow is stabilized. The effect of confinement has previously been studied but not with the inclusion of surface tension. Confinement and surface tension combined cause the transition from convective to absolute instability to occur even with significant coflow. This effect is examined over an infinite domain of density ratios and confinement.
The effect of confinement on the stability of viscous planar jets and wakes
S. J. Rees, M. P. Juniper
Journal of Fluid Mechanics 656 309--336 (2010) doi:10.1017/S0022112010001060
pdf
doi: https://doi.org/10.1017/S0022112010001060
This theoretical study examines confined viscous planar jet/wake flows with continuous velocity profiles. These flows are characterized by the shear, confinement, Reynolds number and shear-layer thickness. The primary aim of this paper is to determine the effect of confinement on viscous jets and wakes and to compare these results with corresponding inviscid results. The secondary aim is to consider the effect of viscosity and shear-layer thickness. A spatio-temporal analysis is performed in order to determine absolute/convective instability criteria. This analysis is carried out numerically by solving the Orr?Sommerfeld equation using a Chebyshev collocation method. Results are produced over a large range of parameter space, including both co-flow and counter-flow domains and confinements corresponding to 0.1 < h2/h1 < 10, where the subscripts 1 and 2 refer to the inner and outer streams, respectively. The Reynolds number, which is defined using the channel width, takes values between 10 and 1000. Different velocity profiles are used so that the shear layers occupy between 1/2 and 1/24 of the channel width. Results indicate that confinement has a destabilizing effect on both inviscid and viscous flows. Viscosity is found always to be stabilizing, although its effect can safely be neglected above Re = 1000. Thick shear layers are found to have a stabilizing effect on the flow, but infinitely thin shear layers are not the most unstable; having shear layers of a small, but finite, thickness gives rise to the strongest instability.
We performed some quick experiments to demonstrate that the sinuous wake mode was enhanced when a slow-moving jet of water was confined within a fast-moving jet of air (this was never published):

Effect of confinement
These images show a coaxial injector consisting of a slow-moving water stream within a fast-moving air stream. The tube ejecting water remains stationary as the tube ejecting air is extended downstream of it. This creates a region of confined flow just downstream of the water injector, which enhances the wake-like oscillation that can be seen in the water jet
Credit: Matthew Juniper
The above analyses were local -- i.e. they were applied to parallel shear flows. Concurrently, Outi Tammisola had been performing global stability analysis on confined non-parallel shear flows (Tammisola et al 2011, J. Fluid Mech. 675, 397–434). She had found the opposite effect: that confinement stabilized her low Reynolds number flows. We investigated this apparent discrepancy and discovered that there are actually three competing effects: (i) confinement modifies the length of any recirculating zone (ii) confinement brings the boundary layers closer to the shear layers, which changes their stability (iii) confinement makes the flow more absolutely unstable when the confinement parameter is close to 1. Depending on the flow parameters, these effects can work together or against each other to stabilize or destabilize the flow.
The local and global stability of confined planar wakes at intermediate Reynolds number
M. P. Juniper, O. Tammisola
Journal of Fluid Mechanics 686 218--238 (2011) doi:10.1017/jfm.2011.324
pdf
doi: https://doi.org/10.1017/jfm.2011.324
Base flow data (Matlab format)
Global mode data (Matlab format)
The large-scale coherent motions in a realistic swirl fuel injector geometry are analysed by direct numerical simulations (DNS), proper orthogonal decomposition (POD), and linear global modes. The aim is to identify the origin of instability in this turbulent flow in a complex internal geometry.
The flow field in the nonlinear simulation is highly turbulent, but with a distinguishable coherent structure: the precessing vortex core (a spiraling mode). The most energetic POD mode pair is identified as the precessing vortex core. By analysing the FFT of the time coefficients of the POD modes, we conclude that the first four POD modes contain the coherent fluctuations. The remaining POD modes (incoherent fluctuations) are used to form a turbulent viscosity field, using the Newtonian eddy model.
The turbulence sets in from convective shear layer instabilities even before the nonlinear flow reaches the other end of the domain, indicating that equilibrium solutions of the Navier?Stokes are never observed. Linear global modes are computed around the mean flow from DNS, applying the turbulent viscosity extracted from POD modes. A slightly stable discrete m = 1 eigenmode is found, well separated from the continuous spectrum, in very good agreement with the POD mode shape and frequency. The structural sensitivity of the precessing vortex core is located upstream of the central recirculation zone, identifying it as a spiral vortex breakdown instability in the nozzle. Furthermore, the structural sensitivity indicates that the dominant instability mechanism is the Kelvin-Helmholtz instability at the inflection point forming near vortex breakdown. Adjoint modes are strong in the shear layer along the whole extent of the nozzle, showing that the optimal initial condition for the global mode is localized in the shear layer.
We analyse the qualitative influence of turbulent dissipation in the stability problem (eddy viscosity) on the eigenmodes by comparing them to eigenmodes computed without eddy viscosity. The results show that the eddy viscosity improves the complex frequency and shape of global modes around the fuel injector mean flow, while a qualitative wavemaker position can be obtained with or without turbulent dissipation, in agreement with previous studies.
This study shows how sensitivity analysis can identify which parts of the flow in a complex geometry need to be altered in order to change its hydrodynamic stability characteristics.
This work was taken further by Luca Biancofiore and Francois Gallaire (Biancofiore L, Gallaire F, Pasquetti R, 2012, Influence of confinement on obstacle-free turbulent wakes, Computers and Fluids 58, 27--44 and Biancofiore L, Gallaire F, 2012, Counterpropagating Rossby waves in confined plane wakes, Phys Fluids 24).




