
A little after the turn of the century, there was great interest in non-modal stability analysis as a way to explain bypass transition to turbulence in hydrodynamics. A conventional stability analysis considers the growth (e.g. of perturbation kinetic energy) over infinite time by considering the eigenvalues of the evolution operator. Non-modal stability analysis considers the transient growth over a defined interval of time by considering the singular values of the evolution operator (Trefethen et al, 'Hydrodynamic stability without eigenvalues' Science 261, 578--584). This could explain, for example, why round pipe flow (Hagen-Poiseuille flow) becomes turbulent even though the laminar velocity profile is stable at all Reynolds numbers.
At the time, it was conventional to linearize around a stable steady solution to the Navier--Stokes equations and to examine the non-normality of the linearized evolution operator. A strongly non-normal operator corresponds to a flow that is capable of strong transient growth, despite being linearly stable in the long time limit. Two interesting papers by Sujith's group at IIT Madras had shown that the evolution operator for thermoacoustic systems could be strongly non-normal (Balasubramanian and Sujith, 2008, Phys. Fluids 20, 044103 and Balasubramanian and Sujith, 2009, J. Fluid Mech. 594, 29–57) and therefore that one might find strong transient growth in thermoacoustics as well as in hydrodynamics.
My first paper in this area used nonlinear adjoint looping of a time-delayed thermoacoustic system to find optimal initial states:
With a sufficiently large impulse, a thermoacoustic system can reach self-sustained oscillations even when it is linearly stable, a process known as triggering. In this paper, a procedure is developed to find the lowest initial energy that can trigger self-sustained oscillations, as well as the corresponding initial state. This is known as the ?most dangerous? initial state. The procedure is based on adjoint looping of the nonlinear governing equations, combined with an optimization routine. It is developed for a simple model of a thermoacoustic system, the horizontal Rijke tube, and can be extended to more sophisticated thermoacoustic models. It is observed that the most dangerous initial state grows transiently towards an unstable periodic solution before growing to a stable periodic solution. The initial energy required to trigger these self- sustained oscillations is much lower than the energy of the oscillations themselves and slightly lower than the lowest energy on the unstable periodic solution. It is shown that this transient growth arises due to non-normality of the governing equations. This is analogous to the sequence of events observed in bypass transition to turbulence in fluid mechanical systems and has the same underlying cause. The most dangerous initial state is calculated as a function of the heat-release parameter. It is found that self-sustained oscillations can be reached over approximately half the linearly stable domain. Transient growth in real thermoacoustic systems is 10^5?10^6 times greater than that in this simple model. One practical conclusion is that, even in the linearly stable regime, it may take very little initial energy for a real thermoacoustic system to trigger to high-amplitude self-sustained oscillations through the mechanism described in this paper.
The Web of Science ranked this paper 373 out of 82732 articles (top 0.45%) published between 2010 to 2014 in the field of Mechanics.
The main conclusion of this paper is that transient growth around the steady solution is almost irrelevant to bypass transition (or 'triggering', as it is known in thermoacoustics). Instead, the important characteristic is transient growth around unstable periodic solutions. Using nonlinear adjoint looping, I found the initial state that grew to self-sustained thermoacoustic oscillations from the lowest initial energy (which I called the 'most dangerous initial condition' and which hydrodynamics researchers call the 'minimal seed'). This is entirely different from the initial state that grows fastest around the steady solution. Instead, it is close to the lowest energy point on the unstable periodic solution plus a component in the direction that maximizes transient energy growth around this periodic solution:
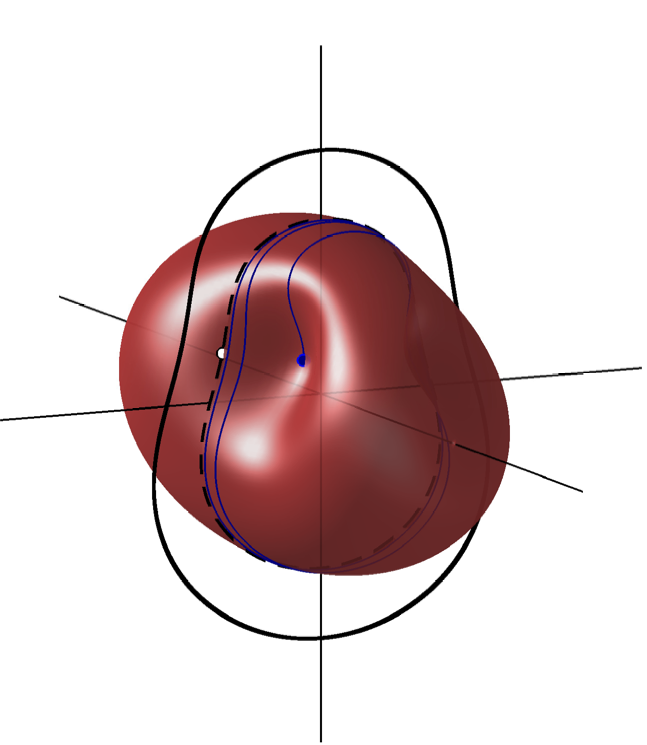
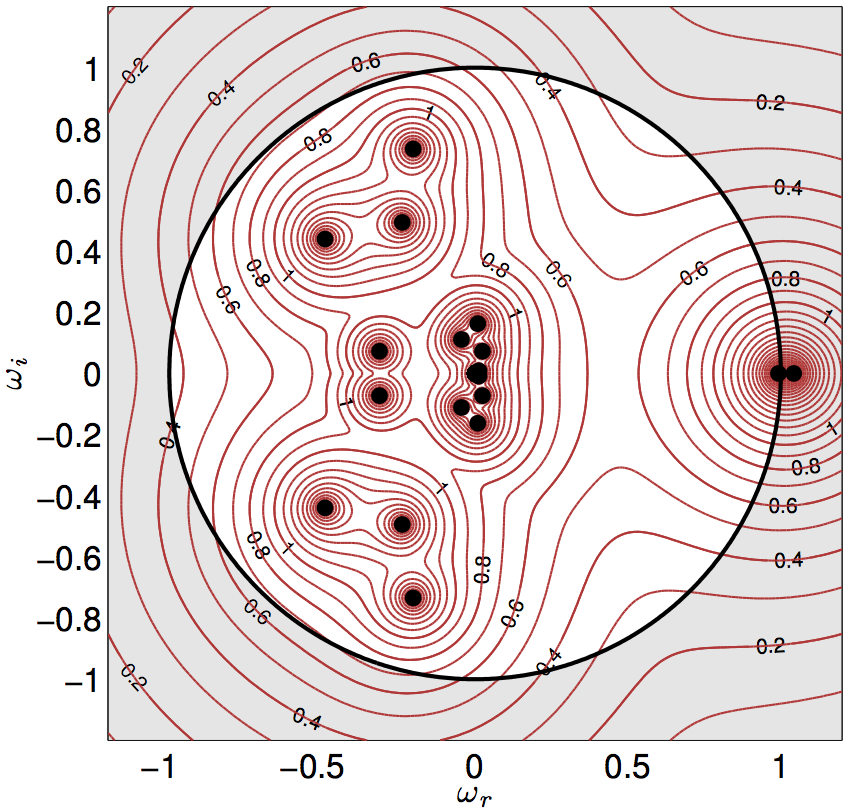
In a second paper, I repeated the analysis over a wider range of initial energies and optimization times, and came to the same conclusion:
This is summarized in a review paper on Triggering in Thermoacoustics
The levels of transient energy growth found in the above analysis, which were of order 1 to 10, were significantly lower than those quoted by Balasubramanian and Sujith. This discrepancy was resolved when Luca Magri found an error in their original paper, showing that transient energy growth in their systems is indeed of order 1 to 10:
With the above analysis, we found the initial states that cause triggering from the smallest initial energy. We found that these states needed most of their energy to be at lower frequencies (around the frequency of the least stable mode) but with some perturbations at higher frequencies. A more interesting experimental question is to find the type of noise that causes triggering from the lowest sound levels. We postulated that 'pink noise', which has more energy at lower frequencies, would be more effective than 'white noise', which has even energy across all frequencies. This did indeed prove to be the case:
This paper explores the analogy between triggering in thermoacoustics and bypass transition to turbulence in hydrodynamics. These are both mechanisms through which a small perturbation causes a system to develop large self-sustained oscillations, despite the system being linearly stable. For example, it explains why round pipe flow (Hagen-Poiseuille flow) can become turbulent, even though all its eigenvalues are stable at all Reynolds numbers.
In hydrodynamics, bypass transition involves transient growth of the initial perturbation, which arises due to linear non-normality of the stability operator, followed by attraction towards a series of unstable periodic solutions of the Navier-Stokes equations, followed by repulsion either to full turbulence or re-laminarization. This paper shows that the triggering process in thermoacoustics is directly analogous to this. In thermoacoustics, the linearized stability operator is also non-normal and also gives rise to transient growth. The system then evolves towards an unstable periodic solution of the governing equations, followed by repulsion either to a stable periodic solution or to the zero solution. The paper demonstrates that initial perturbations that have higher amplitudes at low frequencies are more effective at triggering self-sustained oscillations than perturbations that have similar amplitudes at all frequencies.
This paper then explores the effect that different types of noise have on triggering. Three types of noise are considered: pink noise (higher amplitudes at low frequencies), white noise (similar amplitudes at all frequencies) and blue noise (higher amplitudes at high frequencies). Different amplitudes of noise are applied, both as short bursts and continuously. Pink noise is found to be more effective at causing triggering than white noise and blue noise, in line with the results found in the first part of the paper.
In summary, this paper investigates the triggering mechanism in thermoacoustics and demonstrates that some types of noise cause triggering more effectively than others.
We then examined the influence of noise on the bifurcation diagram and showed, through brute force simulations, that a subcritical bifurcation becomes like a supercritical bifurcation at high noise levels. This was shown later by Tony et al. (Physical Review E 2005 92:062902) by analysing the stochastic governing equations.